Q1. 머신러닝에서의 kmc에 대해

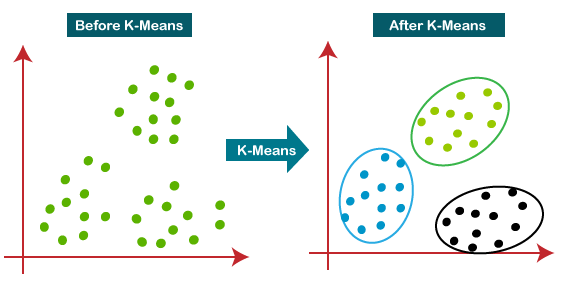
KMC는 K-Means Clustering의 약자입니다. 이는 비지도학습(Unsupervised Learning) 알고리즘 중 하나로,
데이터를 여러 개의 클러스터(Cluster)로 나누는 분석 방법입니다.
K-Means 알고리즘은 클러스터링에서 가장 기본적이고 널리 쓰이는 방법 중 하나입니다.
K-Means Clustering 알고리즘을 사용하면 비슷한 특징을 가진 데이터들끼리 그룹화하여 데이터를 분석할 수 있습니다.
Q2. WSS에 대해



WSS는 Within-Cluster Sum of Squares의 약자로, 한 클러스터 내 데이터들 간 거리의 합을 나타내는 지표입니다.
K-Means Clustering에서는 WSS 값을 최소화하는 것이 클러스터링의 목적 중 하나입니다.
WSS 값이 작을수록 클러스터의 응집도가 높아지기 때문에,
WSS 값을 이용하여 최적의 클러스터 수를 결정하는 Elbow Method를 사용하기도 합니다.
Q3. 실루엣 점수에 대해

[일반적인 설명]
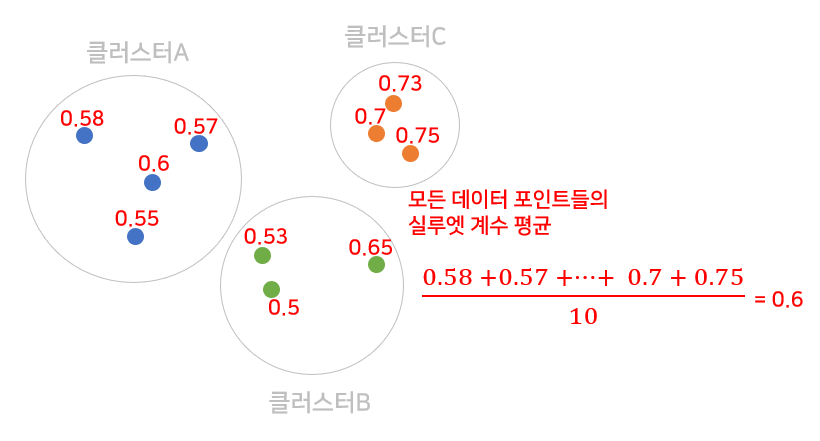
실루엣 점수(Silhouette Score)는 군집화(Clustering)의 성능을 평가하는 지표 중 하나입니다.
각 데이터 샘플의 군집 내 유사성과 군집 간 분리도를 종합적으로 고려하여 계산됩니다.
실루엣 점수는 -1에서 1 사이의 값을 가지며, 값이 클수록 군집화가 잘 되었다는 것을 의미합니다.
만약 실루엣 점수가 음수가 나온다면, 해당 데이터 샘플은 다른 군집으로 분류하는 것이 더 적절합니다.
[초등학생을 위한 설명]
실루엣 점수는 군집화 알고리즘의 성능을 평가하는 지표입니다.
군집화를 할 때, 데이터끼리 비슷한 것끼리 묶어서 그룹을 만듭니다.
이때, 군집 내에서는 서로 더 비슷한 데이터끼리 모이고, 군집 간에는 서로 다른 데이터끼리 모이게 됩니다.
실루엣 점수는 각 데이터가 자신이 속한 군집 내에서 얼마나 잘 맞는지를 측정한 후,
그 값이 얼마나 다른 군집과 다른지를 고려하여 계산됩니다.
만약 실루엣 점수가 높다면, 군집화가 잘 되었다는 것이고, 낮다면 군집화가 잘 되지 않았다는 것입니다.
예를 들어, 학교에서 친구들끼리 얼마나 친한지를 알아보고자 할 때, 비슷한 성격끼리 묶어서 그룹을 만들면 됩니다.
만약, 그룹 내에서는 서로 잘 맞고, 다른 그룹과는 맞지 않는다면 그룹을 잘 만든 것이고,
그렇지 않다면 그룹을 잘 못 만든 것입니다. 이것이 바로 실루엣 점수입니다.
Q4. 오즈비에 대해 (선형회귀와 로지스틱 회귀에서)

초등학생 수준으로 설명하는 방법: 오즈비는 낚시를 예로 들 수 있습니다.
예를 들어, 어떤 호수에서 빨간 물고기와 파란 물고기의 비율이 3 대 1 이라면,
빨간 물고기의 오즈는 3 대 1 이 됩니다. 이때, 파란 물고기의 오즈는 1 대 3 이 됩니다.
즉, 빨간 물고기의 오즈비는 3 대 1 이고, 파란 물고기의 오즈비는 1 대 3 이 됩니다.
이처럼 오즈비는 두 그룹 사이의 비율을 나타내는 지표입니다.
일반적인 설명: 오즈비는 로그 변환을 통해 얻을 수 있는 비율입니다.
로그 변환을 통해 얻은 값은 오즈라고 부릅니다.
로그 변환을 한 이유는 오즈비가 비선형적인 관계를 가지기 때문입니다.
오즈비가 1이면 두 그룹의 성공 확률이 동일하다는 것을 의미합니다.
오즈비가 2이면, 한 그룹의 성공 확률이 다른 그룹의 두 배라는 것을 의미합니다.
오즈비가 0.5이면, 한 그룹의 성공 확률이 다른 그룹의 반으로 줄어든다는 것을 의미합니다.
따라서, 오즈비는 두 그룹의 성공 확률을 비교할 때 유용한 지표입니다.
선형회귀와 로지스틱회귀에서는 오즈비를 통해 각 독립변수가 종속변수에 미치는 영향력을 파악할 수 있습니다.
Q5. 딥러닝에서 0부터 1사이의 값으로 제한이 되는 이유와 시그모이드의 연관지어 2가지 방법으로 설명해줘.
그 중 하나는 내가 초등학생이라 생각하고 비유를 들어서 설명하는거야


0부터 1사이의 값으로 제한하는 이유는 딥러닝에서 발생할 수 있는 수치적인 문제를 해결하기 위함입니다.
예를 들어, 여러 개의 레이어를 거치면서 값이 지수 함수처럼 급격히 커지거나 작아지면서 연산이 불안정해질 수 있습니다. 이를 방지하기 위해 값을 0부터 1사이로 제한하여 연산이 안정적으로 이루어지도록 합니다.
시그모이드 함수는 0부터 1사이의 값을 출력하는 함수로서,
이와 같이 출력값을 제한하는 특성 때문에 딥러닝에서 활용되어 온 것입니다.
초등학생을 예로 들면, 시그모이드 함수는 컵 속에 있는 물의 양을 나타내는 것과 같습니다.
만약 물이 0이면, 컵이 비어있다는 것을 나타내며, 1이면 컵이 꽉 차있다는 것을 의미합니다.
이러한 방식으로 시그모이드 함수는 입력값이 어느 범위 내에 있는지를 나타내기 위해 사용됩니다.
오즈비는 로그 함수의 값으로 나타내는데, 로그 함수는 입력값이 0부터 무한대까지의 값으로 제한되지 않습니다.
따라서 로그 함수를 이용해 오즈비를 계산한 후, 시그모이드 함수를 적용해 0부터 1사이의 값으로 제한하여
사용할 수 있습니다. 이렇게 함으로써 딥러닝에서 안정적인 연산과 오즈비의 활용이 가능해집니다.
Q6. 시그모이드 함수 이해하기1
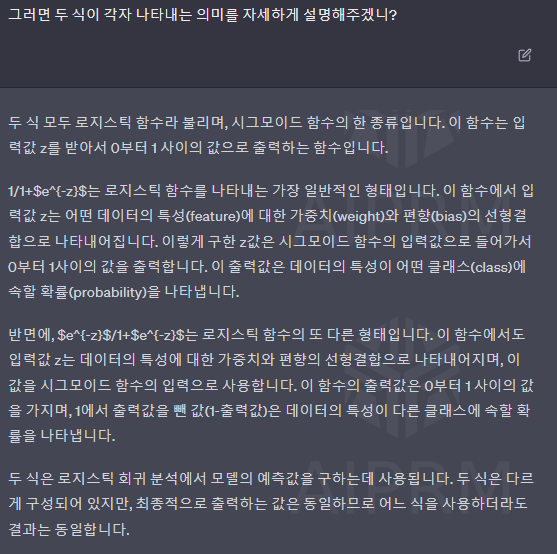
두 식 모두 로지스틱 함수라 불리며, 시그모이드 함수의 한 종류입니다.
이 함수는 입력값 z를 받아서 0부터 1 사이의 값으로 출력하는 함수입니다.
1/1+$e^{-z}$는 로지스틱 함수를 나타내는 가장 일반적인 형태입니다.
이 함수에서 입력값 z는 어떤 데이터의 특성(feature)에 대한
가중치(weight)와 편향(bias)의 선형결합으로 나타내어집니다.
이렇게 구한 z값은 시그모이드 함수의 입력값으로 들어가서 0부터 1사이의 값을 출력합니다.
이 출력값은 데이터의 특성이 어떤 클래스(class)에 속할 확률(probability)을 나타냅니다.
반면에, $e^{-z}$/1+$e^{-z}$는 로지스틱 함수의 또 다른 형태입니다.
이 함수에서도 입력값 z는 데이터의 특성에 대한 가중치와 편향의 선형결합으로 나타내어지며,
이 값을 시그모이드 함수의 입력으로 사용합니다.
이 함수의 출력값은 0부터 1 사이의 값을 가지며, 1에서 출력값을 뺀 값(1-출력값)은
데이터의 특성이 다른 클래스에 속할 확률을 나타냅니다.
두 식은 로지스틱 회귀 분석에서 모델의 예측값을 구하는데 사용됩니다.
두 식은 다르게 구성되어 있지만, 최종적으로 출력하는 값은 동일하므로 어느 식을 사용하더라도 결과는 동일합니다.
Q7. 시그모이드 함수 이해하기 2

두 식은 모두 로지스틱 함수의 일종으로, 어떤 값을 입력하면 0부터 1 사이의 값을 출력하는 S자 형태의 함수입니다.
그러나 두 식은 다르게 유도됩니다.
1/1+$e^{-z}$는 로지스틱 회귀에서 사용되는 시그모이드 함수입니다.
이 함수에서 입력값인 $z$는 어떤 데이터의 특성값들의 가중합과 편향항에 대한 선형 함수입니다.
이를 통해 해당 데이터가 어떤 클래스에 속할 확률을 예측할 수 있습니다.
반면에, $e^{-z}$/1+$e^{-z}$는 오즈비(odds ratio)를 계산할 때 사용됩니다.
오즈비는 어떤 사건이 발생할 확률($p$)과 발생하지 않을 확률($1-p$)의 비율을 나타내는데,
이를 자연로그를 취한 값의 차이(log-odds)로 표현합니다.
이 log-odds 값은 위의 식과 같이 표현할 수 있습니다.
따라서, 두 식은 서로 다른 목적으로 사용되지만, 모두 로지스틱 함수의 형태를 띄고 있습니다.
'배운 책들 정리 > 파이썬 머신러닝 판다스 데이터분석' 카테고리의 다른 글
| 파이썬 머신러닝 판다스 데이터 분석 7-3 - 머신러닝 데이터 분석 - 시그모이드 함수의 식, 로지스틱 회귀, 교차검증 (0) | 2023.05.03 |
|---|---|
| 파이썬 머신러닝 판다스 데이터 분석 6,7 - 데이터프레임의 다양한 응용, 머신러닝 데이터 분석 (0) | 2023.05.01 |
| 파이썬 머신러닝 판다스 데이터 분석 5,6 - 데이터 사전 처리, 데이터프레임의 다양한 응용 (0) | 2023.04.28 |
| 파이썬 머신러닝 판다스 데이터 분석 4_3, 5 - 시각화, 데이터 사전 처리 (0) | 2023.04.27 |
| 파이썬 머신러닝 판다스 데이터 분석 4_2 - 시각화 (0) | 2023.04.26 |



