CP18



Q1) 분산분석과 선형회귀의 차이점
분산분석은 데이터의 분포를 통해 가설에 대한 유의 확률을 찾는 반면
선형회귀는 독립변수의 값이 종속변수에 미칠 가능성을 찾는 것의 차이점이 있다.
Q2)

a) 추측 횟수 바탕 / 응답시간 예측
# 회귀방정식 yhat = bx + a
# 절편(예측변수) + 기울기
회귀방정식 정답 : -0.2141(예측변수) + 17.2021
b) 추측 횟수 8일 / 예측된 응답 시간
-0.2141(8) + 17.2021
= 15.4893
c) 예측치 구하기 (예측된 응답시간 - 실제 응답 시간)
# Load the necessary library
library(tidyverse)
# Read in the dataset
data <- read.csv("data.csv")
# Fit a linear regression model to predict response time based on guess count
model <- lm(response_time ~ guess_count, data = data)
# Add predicted response time to the dataset
data$predicted_response_time <- predict(model, newdata = data)
# Calculate the difference between the predicted response time and the actual response time for each guess count score
data <- data %>%
group_by(guess_count) %>%
summarize(mean_actual_response_time = mean(response_time),
mean_predicted_response_time = mean(predicted_response_time),
mean_difference = mean(response_time - predicted_response_time))
# View the resulting table
data
Q3) 75세 // 알츠하이머 예측 // 예측변수 : 교육수준, 1~10등급 매긴 신체건강지수 // 하지만 다른 변수도 사용할 수 있음
A) 다른 예측변수 사용 시 고려사항 // 그리고 이유까지
종속변수와 관련이 있어야 함. 관련이 없는 예측 변수를 사용할 경우 원하는 연구가설이 귀각이 될 수 있음.
B) 알츠하이머 발병과 관련 있다고 생각 되는 다른 예측 요인 두 가지
독서 시간, 운동 시간
C) 네 가지 예측변수(교육 수준, 일반적인 신체건강지수, 새로 찾은 두 가지 요인)을 사용해 회귀 방정식 모형 그리기.
알츠하이머 병의 유무 = X1 + X2 + X3 + X4 + a
알츠하이머 병의 유무 = 교육 수준 + 일반적인 신체건강지수 + 생활 방식 + 의료 서비스 접근성 + a (기울기)
Q4) 논문 3개 // 예측 변수 2개 이상 포함된 연구 // (독립변수 = 설명변수)
A) 독립변수와 종속변수 확인
1. 음식물쓰레기 종량제 효과성 변화
종속변수 : 배출량
독립변수 : 종량제 시행 여부, 시행 기간, 배출 가격, tools(RFID 종량기기, 행정단속, 주민신고, 인센티브)
2. 향토 음식의 스토리텔링 속성이 구매 태도, 고객 만족도 및 구매 의도에 미치는 영향
종속변수 : 구매태도, 구매 만족도, 구매의도
독립변수 : 흥미성, 지역성,역사성, 독특성, 문화성
3. 비만도와 부정적 비만태도가 비만자기상(像)과 신체존중감에 미치는 영향
종속변수 : 신체 존중감
독립변수 : 비만도, 비만에 대한 부정적 태도
B) 2개 이상의 독립변수가 있다면, 연구자는 이 변수들의 독립성과 관련하여 어떤 주장을 하고 있는지?
1. 음식물쓰레기 종량제 효과성 변화
가설 1 : 음식물쓰레기 배출량과 비용 간 연계성이 강화되면 각 가정에서는 배출 비용을 줄이기 위해서 배출량을 줄이게 될 것으로 예상할 수 있다
연구가설 1에서는 음식물쓰레기 종량제가 배출량에 미치는 영향을 검토 하였다. 종량제를 도입하면 음식물쓰레기 배출량이 유의하게 줄어든다. 종량제를 도입하면 비용 부과 방식이 전환되고 배출 가격이 인상된다. 종량제 도입 이후 음식물쓰레기가 감소하는 현상은 비용 부과 방식의 변화와 배출 가격 인상으로 인하여 주민의 배출량과 수수료 간 연계성에 대한 인 식이 높아진 결과로 볼 수 있다.
가설 2 : 음식물쓰레기 종량제의 효과성은 시행기한이 경과 할수록 점차 감소한다는 예상을 제시할 수 있다
연구가설 2에서는 시간에 따른 종량제의 효과성 변화를 검토하였다. 종량제 시행 전에 비하여 종량제를 시행할 때 음식물쓰레기 배출량이 낮게 나타난다. 하지만 배출량은 종량제를 시행하고 있음에도 불구하고 기간이 경과할 수록 다시 증가하였다. 음식물쓰레기 종량제의 효과가 점차 약화되는 것이다. 이러한 현상이 발생하는 이유는 생활양식의 회귀, 불충분한 유 인, 교육과 홍보 활동 감소 등에서 찾을 수 있다. 한편 종량제의 효과성 저하는 금전적 수단을 통해 친환경적 행동을 유도하려는 방식의 한계를 보여 주는 현상으로 볼 수 있다.
2. 향토 음식의 스토리텔링 속성이 구매 태도, 고객 만족도 및 구매 의도에 미치는 영향
가설 1 : 제주 향토 음식의 스토리텔링 속성은 구매 태도에 유의미한 영향 을 미칠 것이다
첫째, ‘제주 향토 음식의 스토리텔링 속성은 구매 태도에 유의미한 영향을 미칠 것이다’라는 가설 1은 채택되었고, 가설 1의 세부 가설들인 1-a, 1-b, 1-c, 1-d, 1-e 등도 모두 유의미한 것으로 검증되었다.
가설 2 : 제주 향토 음식의 스토리텔링 속성은 고객 만족도에ㅁ 유의미한 영향을 미칠 것이다.
둘째, ‘제주 향토 음식의 스토리텔링 속성은 고객 만족도에 유의미한 영향을 미칠 것이다’라는 가설 2는 채택되었고, 가설 2의 세부 가설인 2-a, 2-b, 2-c, 2-d, 2-e 등도ㅇ 모두 유의미한 것으로 검증되었다.
3. 비만도와 부정적 비만태도가 비만자기상(像)과 신체존중감에 미치는 영향
가설 1. 비만도와 비만자기상 간에 정적 상관이 있을 것이다.
첫째, 비만자기상은 비만도(r = .54), 부정적 비만태도(r = .21) 둘 다와 유의미한 정적 상관이 있는 것으로 나타났다
가설 2. 비만에 대한 부정적 태도는 비만자기상과 정적 상관이 있을 것이다.
비만자기상이 비만도와의 상관만큼은 아니지만, 비만에 대한 부정적인 태 도에도 정적 상관을 보이는 것으로 보아 비만자기상에 비만에 대한 부정적인 태도가 영향을 준다는 것을 확인할 수 있었다. 이는 실제 비만여부와 상관없 이 비만에 대한 부정적인 태도만으로도 신체상 형성에 부정적인 영향을 미칠 수 있음을 의미한다.
C) 세 연구 중 종속변수가 독립변수에 의해 예측 될 수 있음을 밝히는 데 가장 설득력이 부족한 논문은?
그렇게 생각한 이유는?
비만도와 부정적 비만태도가 비만자기상(像)과 신체존중감에 미치는 영향
얻고자 하는 예측 변수 값에 대해서
Q5. 슈퍼볼 우승팀을 예측하는 기회. 1년 동안 승리한 경기평균으로 슈퍼볼 성적을 예측할 수 있는지 궁금했음. 변수 X는 지난 10번의 시즌 동안 승리한 평균 경기 수입니다. 변수 Y는 지난 10년 동안 팀이 슈퍼볼에서 우승했는지 여부.
a) 특정 팀이 슈퍼볼 경기에서 우승한 경험이 있는지에 대한 예측 변수로서 평균 승리 횟수가 유용한지 여부를 어떻게 평가하는지?
# Q5
abs <- data.frame(wins=c(12,11,15,12,13,16,15,9,8,12),
super_bowl_win = c(1,0,0,1,1,0,1,0,0,1))
model <- glm(super_bowl_win ~ wins, data = abs, family = binomial)
cor(abs$wins,abs$super_bowl_win)
이는 상관관계수가 0.204으로 약한 강도로 유의한 모습을 보여주기 때문에 상관성은 있지만 크기가 매우 약해
승리 횟수가 우승 여부를 잘 예측하지 못했다는 결론을 낼 수 있다.
b) 범주형 변수를 종속변수로 사용할 때 얻을 수 있는 이점은 무엇인가?
범위가 -1~1이기 때문에 해석하기 쉽고 값이 높을 수록 변수 간의 연관성이 더 강함을 나타낼 수 있다.
그리고 범주형 변수에 대한 상관 계쑤는 비모수적이기 때문에 데이터의 정규 분포 가정에 의존하지 않는다.
이러한 이유로 유연성이 있어 명목 또는 순서 데이터와 같은 모든 유형의 범주형 변수와 함께 사용할 수 있다.
따라서 탐색적 분석에 유용하다. 그리고 추가 분석을 알려서 상관 계수를 사용하여 관계가 식별되면 회귀 또는 카이제곱 테스트와 같은 추가 분석을 사용하여 관계를 더 깊이 탐색할 수 있다.
추가적으로 어떤 사람이 개를 좋아하는지 고양이를 좋아하는지 여부를 살펴보기 위해서는 범주형 변수를 종속변수로 두어야 하기 때문에 범주형 변수를 연속변수로 사용한다.
c) 종속 변수를 예측하기 위해 사용할 수 있는 다른 변수는 무엇인지? 그 변수를 선택한 이유는?
종속 변수가 지난 10년간 슈펴볼 우승 여부이기 때문에 (범주형 변수) 독립변수인 지난 10년간 승리한 경기의 평균 수 이외에 다른 변수를 뽑자면 홈 경기 출석, 우수 선수 인원, 적은 부상률이 있다.
이는 실적이 좋은 선수의 홈 경기 출석과 적은 부상이 많을 수록 우승 확률이 높을 수 있다는걸 예측하기 때문이다.
Q6. 17장 연습문제 5 - 커피 소비와 스트레스 간의 상관계수에 대한 계산을 확인.
연습문제 5 내용 : 50명 학부생 // 커피 소비 & 스트레스 // 상관계수 0.373 // 유의수준 0.01 //
양측검정 // 상관관계 유의한지? // 진술의 문제점 "커피 적게 마시면 스트레스가 줄어든다는 결론"
커피 소비로 집단 구성원에 대해 예측할 수 있는지 여부 확인
a) 예측변수(독립변수)는? // 원인
커피 소비
b)기준변수(종속변수)는? // 결과
스트레스
c) r^2은?
0.139129상관계수^2 = R^2
0.373^2 = 0.139129
Q7. 훌륭한 요리사가 되기 위한 예측에 대해. 수년간 요리 경험, 교육 수준, 다양한 직책(소스 요리사, 파스타 스테이션 등)과 같은 변수가 모두 위대한 요리사 시험에서 순위에 영향을 미치는 것으로 판단되니 참고하신 후
개별 질문에 대한 대답을 하시오
a) 요리사 시험 점수를 가장 잘 예측하는 것은 어느 것인지?
# Q7
# A)
chef <- data.frame(cooking_career=c(5,6,12,21,7,9,13,16,21,11,15,15,1,17,26,11,18,31,27),
education_level=c(1,2,3,3,2,1,2,2,2,1,2,3,3,2,2,2,3,3,2),
position=c(5,4,9,8,5,8,8,9,9,4,7,7,3,6,8,6,7,12,16),
chef_test_score=c(88,78,56,88,97,90,79,85,60,89,88,76,78,98,91,88,90,98,88))
# Fit linear regression models for each predictor
model1 <- lm(chef_test_score ~ cooking_career, data = chef)
model2 <- lm(chef_test_score ~ education_level, data = chef)
model3 <- lm(chef_test_score ~ position, data = chef)
# Compare coefficients and p-values
summary(model1)
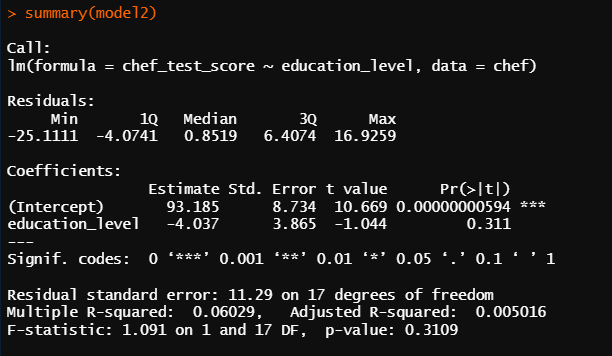
summary(model2)
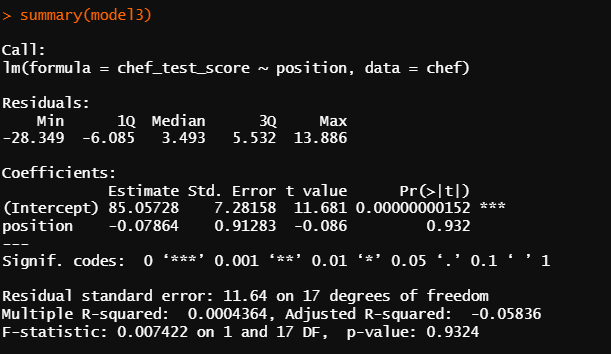
summary(model3)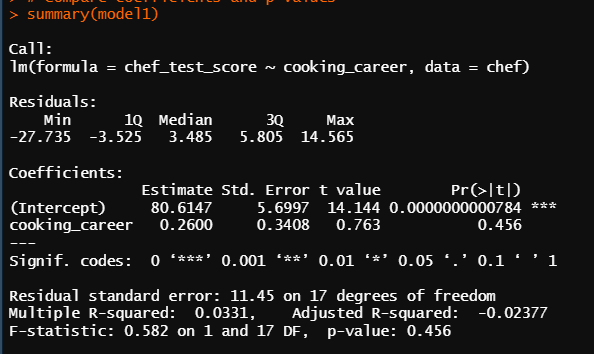
* p-value
cooking_career : 0.456
education_level : 0.311
position : 0.932
그나마 교육 수준이 시험 점수를 가장 잘 예측한다고 하지만 변수 세 개 다 유의하지 않기 때문에
세 개의 항목들이 요리사 시험 점수에 큰 영향을 준다고는 할 수 없다.
b) 12년의 경력이 있고 5개의 직책을 맡은 교육 수준이 2인 사람의 요리사 시험에 대한 기대 점수는 몇 점인지?
# B)
new_data <- data.frame(cooking_career=12, education_level=2, position=5)
expected_score <- predict(lm(chef_test_score ~ education_level + position + cooking_career, data = chef), new_data)
expected_score87.11524

답지와 상이하니 확인 요망
Q8) 18데이터 세트 3 // 교육 수준이 주택 판매 수에 대한 전반적인 예측 (사업 및 교육 수준)에 기여도가 낮은 이유는?
또한 가장 좋은 예측 변수는 무엇이며 이것을 어떻게 알 수 있는지 (힌트 : 일종의 속임수 질문 -> 데이터 분석전 파일의 데이터에서 한 변수가 다른 변수와 상관되는 데 중요한 특성을 찾으시오) 8번도 의미 심장해서 교수님께 문의
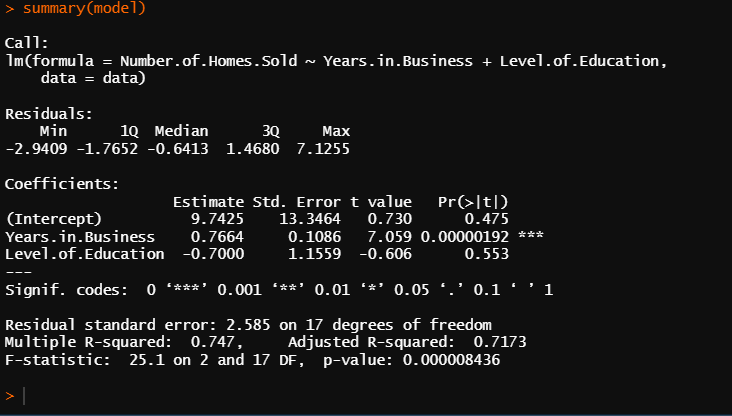
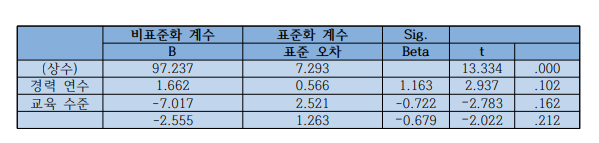
A) 기여도 낮은 이유
잔차 표준 오차(Residual standard error)를 보면 2.585이며 이는 관측된 데이터 포인트가 회귀선에서 떨어지는 평균 거리를 측정한 것인데 이는 변동성이 낮다는 것을 의미한다. 예시로 교육 수준의 계수 추정치인 -0.7000은 교육 수준이 1단위씩 증가할 때마다 다른 모든 변수를 일정하게 유지한 상태에서 판매된 주택 수가 0.7000단위 감소할 것으로 예상됨을 나타낸다. 따라서 p값 0.553은 이 계수가 통계적으로 유의하지 않다는 결론이 나타나 교육 수준이 주택 수에 유의하지 않은 영향을 미친다는 결론을 낼 수 있다. (잔차 표준 오차 값(RSE)이 낮을 수록 예측 값이 실제 값에 가깝다는 것을 의미하기에 모델이 데이터에 더 적합하다는 것을 의미함 = 잔차값이 낮다 = 예측한 값이 데이터 모델에 적합하다)
B) 가장 좋은 예측 변수는?

유의확률 0.001에 해당 되며 p-value 0.00000192에 해당 되는 사업 기간이다.
이것을 어떻게 알 수 있냐면
C) 데이터 분석전 파일의 데이터에서 한 변수가 다른 변수와 상관되는데 중요한 특성을 찾으세요. 앞서 찾은 예측 변수가 가장 좋은 예측변수라는 것을 어떻게 알 수 있는지 연관하여 설명하시오. (다만 가장 좋은 예측변수라는 말 자체가 함정이니 이를 고려하여 설명하시오)
한 변수를 다른 변수와 연관시키는 중요한 특성을 결정하기 위해
일반적으로 두 변수 사이의 선형 관계의 강도와 방향을 측정하는 상관 계수를 살펴보는게 일반적이다.
(상관계수는 -1<=0<=~1의 범위를 나타냄)
다만 앞서 설명한 예측변수가 가장 좋은 예측변수라고 해도 모델에 포함되지 않은 주택 판매 수에 영향을 미치는 다른 변수가 있을 수 있다. 예를 들어 주택 판매 수에 영향을 미치는 요소는 계절성, 시장 동향도 있을 것이기 때문에 사업 기간만을 가지고 가장 좋은 예측 변수라고는 설명할 수 없다.
Q9) 예측변수와 예측된 변수의 어느 조합에서든, 변수 간 관계의 본질을 어떻게 해야 하는지?
변수 간 관계의 본질은 독립적인 두 변수 간의 연관성으로 예측변수의 값을 극대화시켜
변수와 변수 간의 상호관계성을 확인하는 것이 중요하다. 따라서 공통점이 있는 변수가 아닌 변수와 변수 간의
연관성이 있는 변수를 확인하여 예측 변수의 값을 극대화시키도록 변수 설정을 잘 해야 한다.
CP19


Q1 카이제곱 0이 되는 이유, 예시
카이제곱 값이 0인 경우는 테스트 중인 두 변수 간에 연관성이 없음을 나타낸다. 예를 들어 서양인의 머리색깔 변수와 김치 변수를 가지고 김치를 먹을 수록 머리색깔이 노랗게 변한다는 가설을 설정할 때 연관성이 없을 수 있다.
Q2 최근 선거에서 같은 수의 소속 정당원들이 투표했는지 여부를 유의수준 0.05에서 검정하시오
# CP19
# create a vector with the observed values
observed <- c(800, 700, 900)
# perform the chi-square test
test <- chisq.test(observed)
# print the results
test
# calculate chi-square test statistic
chi_sq <- sum((observed - expected)^2/expected)
# calculate p-value
df <- length(observed) - 1
p_value <- 1 - pchisq(chi_sq, df)
p_value
p_value < 0.05
# get the threshold for rejecting the null hypothesis
threshold <- qchisq(0.05, df = length(observed) - 1, lower.tail = FALSE)
threshold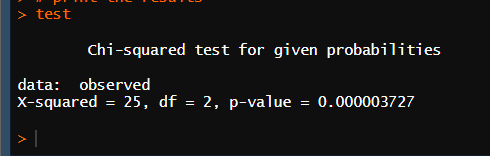
0.05 수준에서 자유도가 2인 경우 귀무가설을 기각하는데 필요한 임계값은 5.99이며 카이제곱 검정값은 25.00이다. 따라서 카이제곱 검정값이 임계값을 넘어갔기 때문에 귀무가설을 귀각한다. 추가로 p-value 값이 0.000003727로 유의수준보다 높기 때문에 같은 수의 소속 정당원들이 투표했다는 연구가설을 채택한다.
Q3. 남학생(1), 여학생(2)이 0.01 유의수준에서 축구 활동에 참여하는지 여부 확인
# Q3
data <- read.csv("./Syntax(R)/19/ch19ds3.csv")
t <- table(data$Gender)
# 차이검정
chisq.test(t)
# 임계값
qchisq(0.01, df = length(t)-1, lower.tail = FALSE)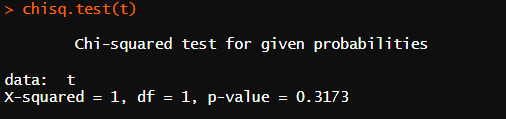

0.01 유의수준에서 자유도 1인 경우 귀무가설 기각하는데 필요한 임계값은 6.64이며 획득된 값은 1.00이므로 귀무가설을 기각할 수 없다. 이는 축구 활동에 참여하는 남학생과 여학생의 수에 차이가 없음을 의미한다.
Q4. 새로운 분포가 예상했던 대로인지 확실하지 않다. 0.05 수준에서 적합도에 대해 다음 데이터를 검정하시오.
# Q4
student <- c(309,432,346,432,369,329)
# 카이제곱 검정
test <- chisq.test(student)
test
# 임계값
qchisq(0.05, df = length(student)-1, lower.tail = FALSE)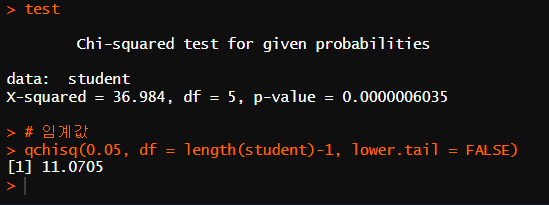
차이 제곱 검정에서 나온 36.98이 임계값 11.07을 넘었기 때문에 학년별로 등록 인원이 예상했던 숫자가 아니라는 결론이 나온다. (임계값이라는 예상치와 다르니 귀무가설 기각)
Q5. 막대사탕 맛이 거의 같다고 주장함. 나머지 절반은 동의하지 않음. 누구 말이 맞을까?
# Q5
data <- read.csv("./Syntax(R)/19/ch19ds4.csv")
# 카이제곱검정
test<- table(data$Preference)
chisq.test(test)
# 임계값
qchisq(0.05, df = length(test)-1, lower.tail = F)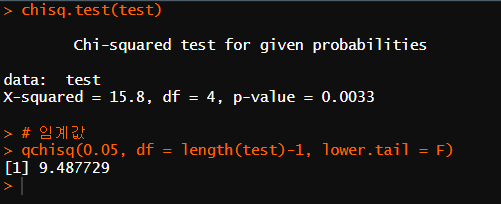
임계값 9.49에서 카이제곱 검정이 15.8으로 귀무가설이 기각이 되어 일반적으로 맛이 같다는 사람들의 예상과는 다르게
맛에 따라 선호도 수의 차이가 유의하기 때문에 맛의 차이가 있는 것으로 확인할 수 있었음. 유의 수준 0.05에서 p-value가 0.0033에 가까울 정도로 선호도 차이가 눈에 띄는 것으로 보아 맛의 차이가 있음을 눈에 띄게 확인할 수 있음.
Q6. 변수들의 관련성 확인
# Q6 (2개 이상)
# Create the contingency table
choc_table <- matrix(c(160, 400, 175, 150, 500, 250), nrow = 2, byrow = TRUE, dimnames = list(c("Basic", "Peanut"), c("High", "Medium", "Low")))
choc_table
# Perform the chi-square test
chisq_result <- chisq.test(choc_table)
chisq_result
# Create the difference test table
prop.table(choc_table, 1)
# Obtain the threshold value
qchisq(0.05, df = chisq_result$parameter, lower.tail = FALSE)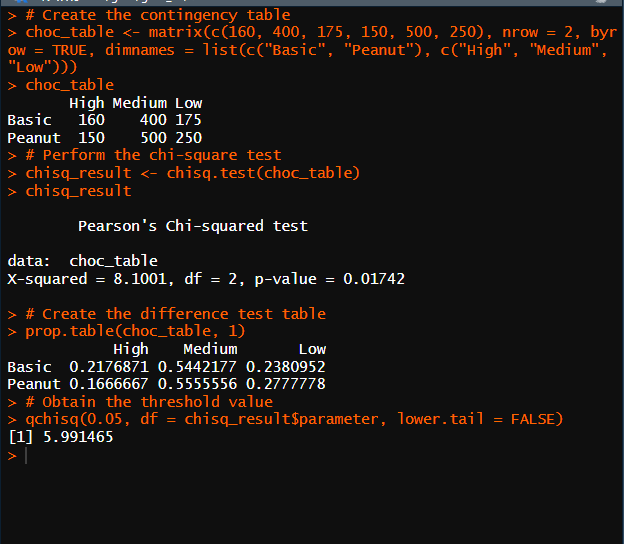
카이제곱 값이 8.1이고 자유도가 2일 때 임계값이 6.0이기 때문에 귀무가설을 귀각한다. 실제로 운동 수준에 따라 기본 맛 또는 땅콩 맛을 선호한다는 결론을 내릴 수 있을 만큼 p 값 또한 0.01742에 해당할 만큼 크다고 볼 수 있다.
Q7 데이터 세트에 포함된 나이와 근력수준의 두 가지 변수 항목이 있는데 이 두 요소가 서로 독립적인가요?
# Q7
data <- read.csv("./Syntax(R)/19/ch19ds5.csv")
# 테이블 변환
a.s_tb <- table(data$Age, data$Strength)
a.s_tb
# 차이제곱 검정
c_t<- chisq.test(a.s_tb)
c_t
# Obtain the threshold value
qchisq(0.05, df = c_t$parameter, lower.tail = FALSE)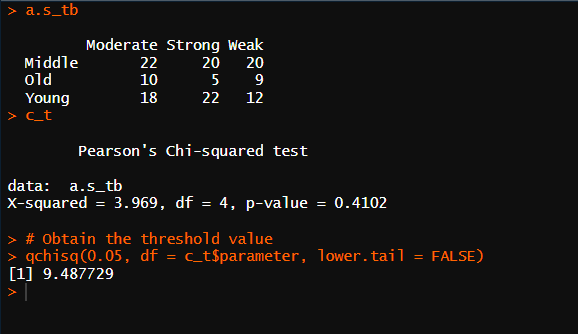
자유도 4, 그리고 임계값 9.49로 카이제곱 값이 3.969은 0.41수준에서 유의하다.
따라서 귀무가설에 해당되므로 두 변수 간의 관계성이 없고 그 말은 두 변수가 각각 독립성이 없다는 말이다.
'개인공부 정리 > 문제풀이' 카테고리의 다른 글
| 0510 자바 정석 연습 문제 - 연산자, 조건문 (수정중) (0) | 2023.05.11 |
|---|---|
| CP7,CP17 문제 풀이 (0) | 2023.02.20 |
| CP9 ~ CP11 문제 풀이 (수정중) (0) | 2023.02.17 |
| CP12 ~ CP15 문제 풀이(수정중) (0) | 2023.02.17 |
| CP3 ~ CP5 문제 풀이 (0) | 2023.02.16 |


