CP1~C2는 일반적인 정의를 기술한 문제라 스킵
CP3
# CP3 - Q1,Q2,Q3,Q4
mydata <- c(513,545,354,675,873)
is(mydata)
summary(mydata)
data <- read.csv("./Syntax(R)/03/ch3ds1.csv")
summary(data)
Q1. Rstudio에 있는 4개의 분할 창은 무엇이며 각 분할 창의 기능은 무엇인가요
RStudio는 R 프로그래밍 언어에 사용되는 통합 개발 환경(IDE)입니다. 각각 특정 기능이 있는 4개의 창 또는 창으로 구성됩니다.
- 소스: 소스 창은 R 코드를 작성하고 편집할 수 있는 곳입니다. 구문 강조 및 코드 완성과 같은 기능을 제공하여 코드를 보다 효율적으로 작성할 수 있도록 도와줍니다.
- 콘솔: 콘솔은 명령을 입력하고 출력을 볼 수 있는 곳입니다. 여기에서 R 환경과 상호 작용할 수 있으며 코드 결과가 표시됩니다.
- 환경/기록: 환경/기록 창에는 현재 R 환경에 있는 개체 및 데이터에 대한 정보가 표시됩니다. 또한 콘솔에 입력한 명령의 기록도 제공합니다.
- 파일/플롯/패키지/도움말: 파일/플롯/패키지/도움말 창에서는 파일과 디렉토리를 탐색하고 플롯을 보고 설치된 패키지를 관리할 수 있습니다. R 기능 및 패키지에 대한 도움말 파일 및 문서에 액세스하는 데 사용할 수도 있습니다.
Q2. Rstudio 콘솔에 입력한 과거 명령을 보려면 어느 분할 창의 어떤 탭을 클릭해야 합니까
과거에 입력한 Rstudio 콘솔 명령어를 확인하려면 "History" 탭을 클릭해야합니다. "History" 탭은 RStudio Editor 창 옆에 위치한 "Console" 창 내에서 하위 탭으로 표시됩니다. 이 탭에서 이전에 실행된 모든 명령을 볼 수 있으며 필요한 경우 다시 실행할 수도 있습니다.
Q3. Rstudio에서 다음과 같은 간단한 데이터 세트를 입력하고 이름을 정하세요.
513, 545, 354, 6751. 사용할 Rsudio 명령은 무엇입니까?
my_data <- c(513, 545, 354, 675)
2. Is() 함수를 사용하여 작업 공간의 객체를 나열하세요.
is(mydata)3. summary 명령을 사용하여 데이터 요약을 생성하세요.
summary(mydata)

Q4. Rstudio에서 3장 데이터 세트1(ch3ds1.csv)을 읽고 데이터 세트 이름을 ch3ds1로 정하세요. 그리고 해당
데이터 세트의 요약(summary)을 생성하세요
data <- read.csv("./Syntax(R)/03/ch3ds1.csv")
summary(data)
CP4
# CP4 - Q1~Q11
# Q1,Q2
data <- read.csv("./Syntax(R)/04/ch4ds2.csv")
summary(data)
summary(as.factor(data$Score.1));
summary(as.factor(data$Score.2));
summary(as.factor(data$Score.3))
# Q3
data <- read.csv("./Syntax(R)/04/ch4ds3.csv")
mean(data$Number.of.Beds);mean(data$Infection.Rate)
# Q4
data1 <- c(20,18,25,19,17,20)
data2<- c(2.95,1.49,3.50,2.95,1.99,1.99)
sum(data1*data2)
mean(data2)
# Q5
data1 <- c(323.6,234.6,308.3)
data2 <- c(3454,5645,4565)
data3 <- c(4534,6765,6654)
summary(data1);summary(data2);summary(data3)
mean(data1);mean(data2);mean(data3)
# Q6
data1 <- c(4,4,5,4)
data2 <- c(2,1,2,1)
data3 <- c(4,3,3,3)
data4 <- c(3,4,4,5)
data5 <- c(5,5,5,4)
summary(data1);summary(data2);summary(data3);summary(data4);
summary(data5)
sum(data1);sum(data2);sum(data3);sum(data4);sum(data5)
# Q10
data <- read.csv("./Syntax(R)/04/ch4ds4.csv")
str(data)
subset_data <- subset(data, Group %in% c(1,2,3))
tapply(subset_data$Attitude, subset_data$Group, mean)
# Q11
data1 <- c(12,14,18,27)
data2 <- c(21,15,14,12)
data3 <- c(7,12,21,15)
data1 <- c(12,21,7)
data2 <- c(14,15,12)
data3 <- c(18,14,21)
data4 <- c(27,12,15)
mean(data1);mean(data2);mean(data3);mean(data4)

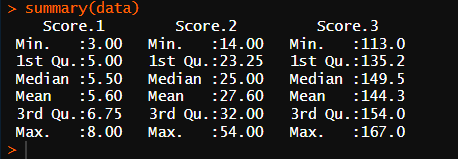
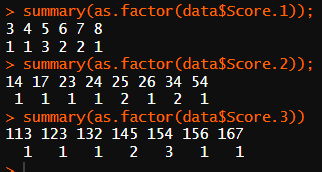
Q1//Q2
* 점수 1
평균 : 5.60
중앙값 : 5.50
최빈값 : 5
* 점수 2
평균 : 27.60
중앙값 : 25.00
최빈값 : 25, 34
* 점수 3
평균 : 144.3
중앙값 : 149.5
최빈값 : 154

Q3.

Q4. 각 메뉴의 가격 평균, 총 매출액, 많이 팔린 아이템
각 메뉴의 평균 가격이 2.47달러이고 총 매출액 303달러이고 가장 많이 팔린(최빈값) 메뉴는
치킨 버거입니다.
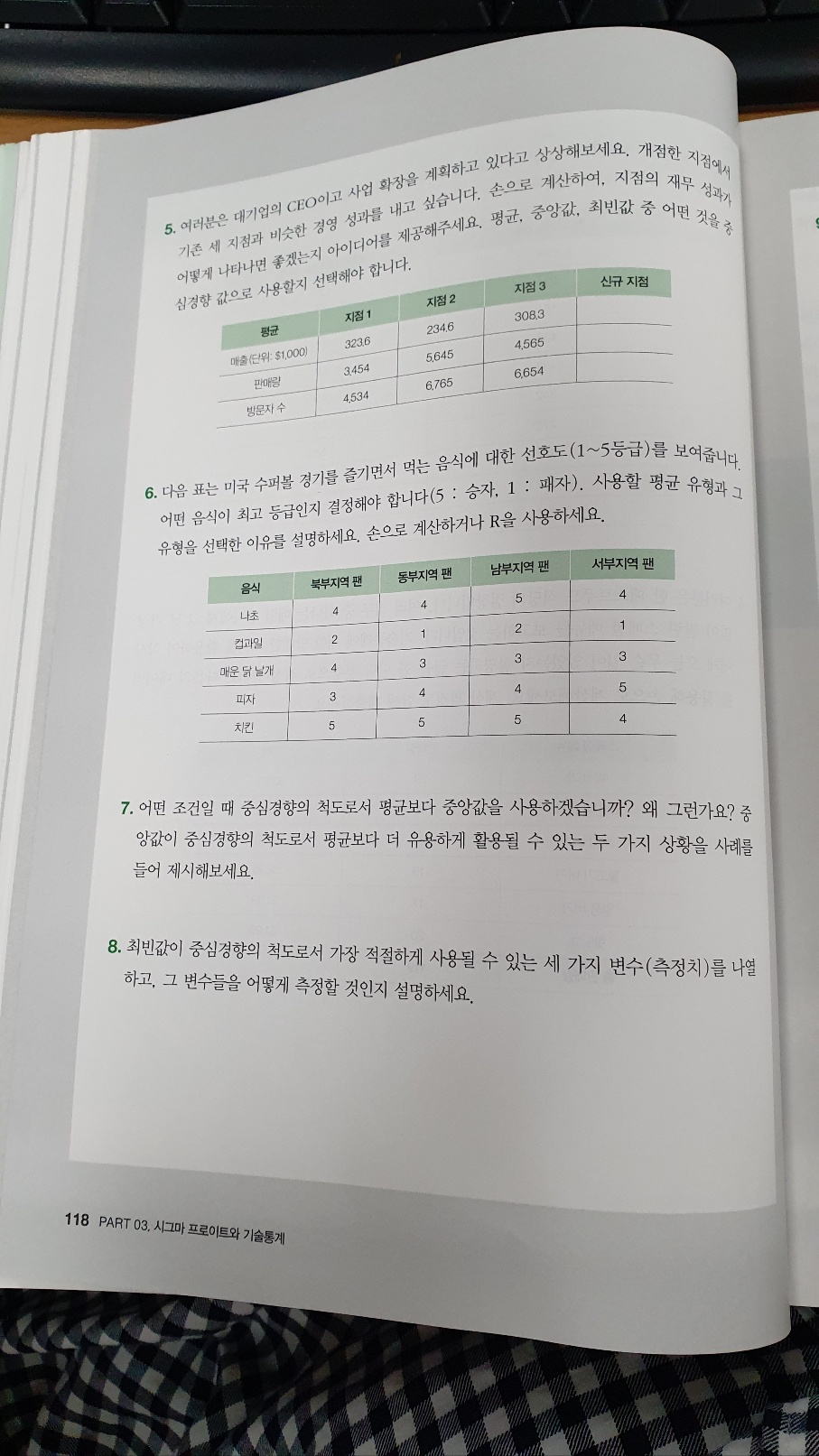
Q5.
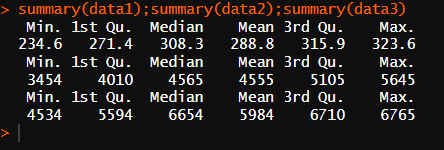
매출 : 288.8
판매량 : 4555
방문자수 : 5984
평균, 중앙값, 최빈값이 있지만 일단 평균치를 만족시키는게 사업확장에서 안정적일 것으로 보인다.
Q6.
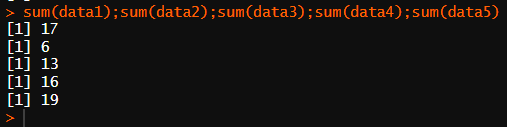
최빈값을 기준으로 했을 때 치킨이 최고등급이고
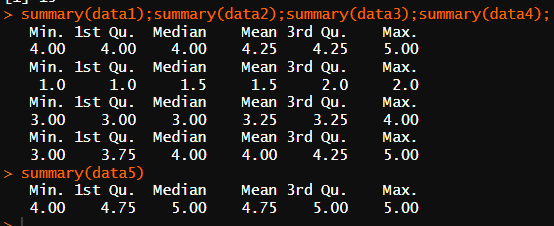
평균값을 기준으로 했을 때도 평균값이 높은 그룹은 치킨으로 나왔다.
Q7.
중심경향의 척도로 중앙값을 기준으로 좌우 면적의 범위가 대칭을 이루기 때문에 중앙값을 선택할 것이다.
* 사례
1) 편향된 데이터 : 평균은 이상치의 영향을 많이 받지만 중앙값은 이상치에 영향을 많이 받지 않는다.
예시로 가계 소득 데이터에서 소수의 고소득자가 있다면 평균을 상향 왜곡할 수 있지만
중앙값을 기준으로 한다면 영향을 받지 않는다.
2) 서수 데이터 : 7점 척도와 같은 데이터를 활용할 때 평균값보다 중앙값이 중심 경향을 더 적절하게 측정한다.
3) 극단값이 있는 데이터 : 1번과 같은 이유로 금융 데이터와 같이 극단값이 있는 데이터 세트에서 중앙값은
극단값 크기에 영향을 받지 않기에 중심 경향을 더 잘 측정할 수 있다.
Q8. 중심경향의 척도로서 최빈값이 가장 적절하게 사용될 수 있는 세가지 변수(측정치)를 나열하고, 그변수들을 어떻게 측정할 것인지 설명하세요.
- 명목 변수: 값으로 범주 또는 레이블이 있는 변수입니다. 명목 변수의 예로는 성별(남성, 여성), 인종(백인, 아프리카계 미국인 등), 자동차 유형(세단, SUV 등)이 있습니다. 명목 변수의 가장 빈번한 값을 측정하려면 각 범주 또는 레이블의 발생 횟수를 세고 어떤 것이 가장 자주 나타나는지 확인하기만 하면 됩니다.
- 서열 변수: 순서를 지정하거나 순위를 매길 수 있는 범주 또는 레이블이 있는 변수입니다. 순서형 변수의 예로는 교육 수준(고등학교, 대학, 대학원), 소득 수준(낮음, 중간, 높음) 및 고객 만족도(매우 만족, 다소 만족, 다소 불만족, 매우 불만족)가 있습니다. 순서 변수의 가장 빈번한 값을 측정하려면 먼저 순위 또는 순서(예: 고등학교의 경우 1, 대학의 경우 2, 대학원의 경우 3)에 따라 각 범주 또는 레이블에 숫자 값을 할당합니다. 그런 다음 각 숫자 값의 발생 횟수를 세고 어떤 값이 가장 자주 나타나는지 결정합니다.
- 불연속형 변수: 특정 정수 값만 취할 수 있는 변수입니다. 이산형 변수의 예로는 가족의 자녀 수, 한 가구가 소유한 자동차의 수, 회사의 직원 수 등이 있습니다. 불연속 변수의 가장 빈번한 값을 측정하려면 각 가능한 값의 발생 횟수를 세고 어떤 값이 가장 자주 나타나는지 확인하면 됩니다.
모든 경우에 가장 빈번한 값은 데이터를 요약하고 해당 특성을 이해하는 데 유용할 수 있는 중심 경향의 척도를 제공합니다. 그러나 가장 빈번한 값이 항상 중심 경향에 대한 최선의 또는 가장 유용한 측정이 아닐 수 있으며 데이터의 특정 특성에 따라 평균 또는 중앙값과 같은 다른 측정이 더 적절할 수 있음을 기억하는 것이 중요합니다.
Q9.
중앙값으로 계산하는게 적절한 중심경향 척도로 생각한다. 왜냐하면 최고값과 직전 최고값의 차이가 크기 때문에
중앙값을 이용해서 중심경향 척도를 판별해야 한다.
Q10.
data <- read.csv("./Syntax(R)/04/ch4ds4.csv")
str(data)
subset_data <- subset(data, Group %in% c(1,2,3))
tapply(subset_data$Attitude, subset_data$Group, mean)
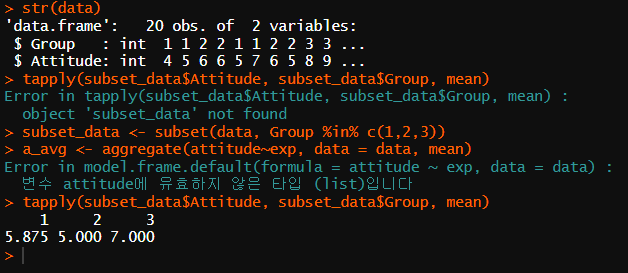
* 평균 태도 점수
그룹 1 : 5.9
그룹 2 : 5
그룹 3 : 7
Q11
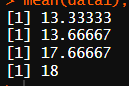
1주차 13.5
2주차 13.7
3주차 17.7
4주차 18
CP5



Q1. 왜 범위가 분산의 가장 편리한 측정 수단이면서 동시에 가장 부정확한 측정 수단일까요? 범위를 언제 사용하겠습니까?
데이터 세트의 변동성을 빠르게 표기하기 때문에 가장 편리하고 간단한 분산 측정법이지만 변동성을 고려하지 않기 때문에 범위로만 측정하기에는 가장 부정확한 분산 측정값이기도 하다. 범위는 일반적으로 이상치에 영향을 많이 받는데 범위는 데이터의 변동성을 정확하게 반영하지 않기 때문이다.
그래서 범위를 사용하는 경우는 데이터를 빠르게 측정할 경우나 적은 수의 값을 가진 작은 데이터 세트를 작업할 때 주로 사용한다.
Q2. 배타적 범위와 포용적 범위를 계산하세요.
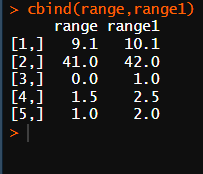
배타적 범위를 구하기 위해서는 포용적 범위식에서 +1을 더해야한다. (배타적 범위는 최솟값과 최댓값 까지 포함하기에)
배타적 범위 = (최대값 - 최소값) + 1
포용적 범위 = 최대값 - 최소값
1 - 배타적 범위 : 9.1 포용적 범위 : 10.12 - 배타적 범위 : 41.0 포용적 범위 : 42.03 - 배타적 범위 : 0 포용적 범위 : 1.0
4 - 배타적 범위 : 1.5 포용적 범위 : 2.5
5 - 배타적 범위 : 1.0 포용적 범위 : 2.0
Q3. 대학 신입생의 성격 측정치가 신장(키) 측정치보다 변동성이 더 큰 이유는 무엇일까요?
키는 성장판이 닫히면 일정적인 수치를 유지하는 반면 성격은 환경이 변함에 따라 변동성의 폭이 크고 키처럼 객관적으로 판단하는게 아닌 자기가 생각하는 모습을 통해 점수를 매기는 것이기 때문에 주관적인 데이터라 변동성이 크다.
신장은 수치화할 수 있지만 성격은 다양한 요인에 의해 영향을 받을 수 있는 복잡한 구조이기 때문이다.
키는 유전학에 의해 결정 되며 시간이 지남에 따라 변화에 덜 민감합니다. 또한 성격 특성은 응답 편향, 측정 오류의 원인이 될 수 있는 설문지를 통해 평가 되기 때문에 정확성이 많이 떨어진다. 그리고 키는 시간이 지나면서 안정적으로 유지되는 경향을 띄는 반면 성격은 상황에 따라 단기적으로 변동될 수 있기 때문에 변동성의 다양성을 띈다.
Q4. 한 집단에 속한 개인들의 시험 점수가 비슷할수록 표준편차가 더 작아지는 이유는 무엇일까요? 또한, 관측치의 수가 더 많은 집단이 더 적은 집단보다 측정값들의 변동량이 상대적으로 더 적을 것으로 예상하는 이유는 무엇입니까?
표준 편차는 데이터의 분산 정도를 나타내는 척도이기 때문에 시험 점수가 비슷하면 데이터 포인트가 가까이 있다는 것을 의미한다. 이는 분산이 작아진다는 소리이며 따라서 시험 점수가 비슷하다는 의미는 분산의 폭이 작다는 의미이며 표준편차가 작아진다는 의미이다. (변동량의 크기는 분산 폭의 비례한다)
또한 관측치의 수가 많다는 것은 분산의 폭이 작아 데이터 포인트 사이사이의 간격이 작다는 것을 의미하며 변동량의 크기는 분산의 폭에 따라 비례하기 때문에 관측치의 수가 더 많을 수록 분산의 폭이 작아 분산의 폭이 큰 적은 집단보다 변동량이 상대적으로 더 적을 것이다.
Q5. 다음 점수에 대한 범위 ,불편추정 표준편차(편향되지 않은 표준편차), 편의추정 표준편차, 분산을 계산하세요. 수식을 이용해 직접 손으로 계산하세요.
data <- c(94, 86, 72, 69, 93, 79, 55, 88, 70, 93)
* 조건 및 설명
1) 불편이라는 뜻은 편향되지 않다는 것을 의미함. 이는 분모에 n-1을 통해서 구해준다.
2) 분산과 표준편차에서 표준편차는 sqrt를 씌워서 루트를 씌워주지만 분산은 루트를 씌우지 않는다.
(따라서 분산이 더 큰 값)
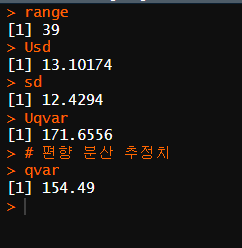
배타적 범위는 39입니다. 불편 표본 표준편차는 13.10입니다. 편의 표준편차는 12.42입니다. 이렇게 차이가 나는 이유는 편향된 추정의 경우 표본 크기 10으로 나누고, 불편 분산 추정치는 171.66이고 편향 추정치 는 154.49입니다.
Q6. 연습문제 5에서 불편추정치가 편의추정치보다 더 큰 이유는 무엇입니까?
불편 추정치는 보수적이며 의도적으로 통계 값을 과대 평가하기 때문에 항상 편향 추정치보다 값이 크다.
편향되지 않은 추정치를 구하기 위해서는 분모의 값을 줄여줘야하기 때문에
분모의 값을 n이 아닌 n-1로 계산하며 따라서 불편추정치가 더 클 수 밖에 없다.
Q7. R을 사용하여, 한 학기 동안 치른 세 가지 시험 점수 데이터 세트에 대한 기술통계를 계산하세요. 어떤 시험의 평균 점수가 가장 높습니까? 변동성이 가장 적은 시험은 무엇입니까? (변동성을 알기 위해서는 표준편차를 구해야 함)
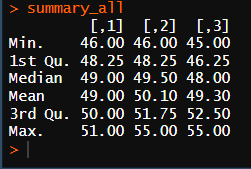
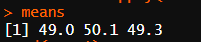

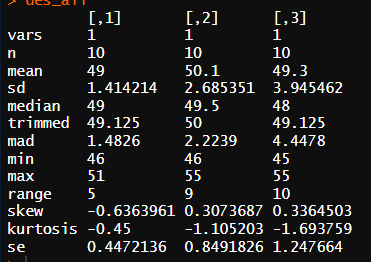
평균값이 가장 높은 점수는 50.1로 test 2이다.
변동성이 가장 적은 시험은 표준편차 1.41의 값을 가지고 있는 test 1이다.
Q8. 표준편차 및 분산의 불편추정치 구하기.
data <- c(58,56,48,76,69,76,78,45,66)
* sd 함수는 n-1로 불편 추정치를 기준으로 함.
* 표준편차 또한 바로 불편 추정치를 기준으로 함.
표준편차 : 12.39
분산 : 153.53
Q9. 분산 36에 대한 표준편차와 범위
표준편차 : 6
범위 : 구할 수 없음 -> 표준편차와 분산값으로만 범위를 알 수는 없다.
Q10. 포용적 범위, 표본 표준편차, 표본 분산 계산
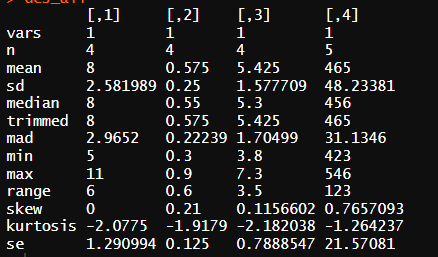
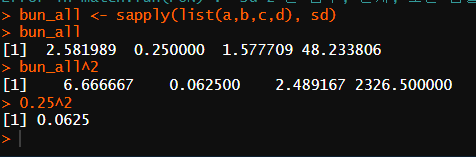
* a
범위 : 6
표준편차 : 2.58
분산 : 6.67
* b
범위 : 0.6
표준편차 : 0.25
분산 : 0.06
* c
범위 : 3.5
표준편차 : 1.58
분산 : 2.49
* d
범위 : 123
표준편차 : 48.23
분산 : 2,326.5
Q11. 키와 몸무게에 대한 모든 변동량 계산. (변동량을 구하라는 뜻은 표준편차, 분산, 범위를 구하라는 뜻)
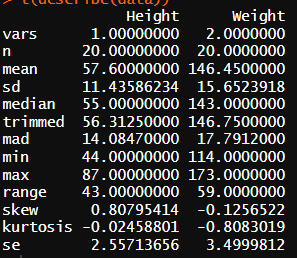
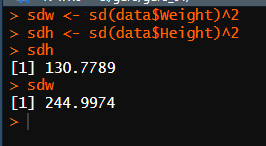
* 키
표준편차 : 11.44
분산 : 130.78
범위 : 43
* 몸무게
표준편차 : 15.65
분산 : 245
범위 : 59
Q12. R이 계산한 표준편차 값이 불편추정치인지, 편의추정치인지 어떻게 알 수 있는가?
SD 함수를 사용한 것과 실제 식을 대입해서 불편추정치 또는 편의추정치를 구해보면
sd 함수를 사용하면 n-1 값으로 구했다는 것을 알 수 있다.
Q13. 표준편차, 분산의 편의추정치 및 불편추정치 계산
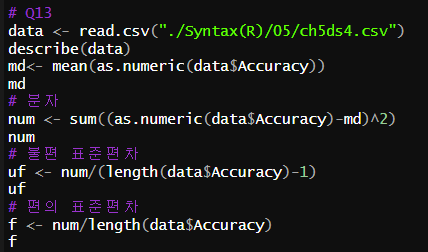
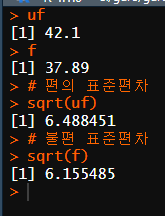
불편 표준편차 : 6.49
편의 표준편차 : 6.15
분산 불편추정치 : 42.1
분산 편의추정치 : 37.89
편의가 n-1을 하지 않았기 때문에 더 크다.
Q14.
시험 점수 집합의 각 점수가 평균 값에서 0.94 수치의 표준편차 만큼 떨어져있다는 뜻을 의미한다.
C6~C8은 스킵
'개인공부 정리 > 문제풀이' 카테고리의 다른 글
| CP9 ~ CP11 문제 풀이 (수정중) (0) | 2023.02.17 |
|---|---|
| CP12 ~ CP15 문제 풀이(수정중) (0) | 2023.02.17 |
| 0210 오라클 DB 문제풀이 - 커서와 예외처리, 트리거 (0) | 2023.02.10 |
| 0209 오라클 DB 문제풀이 - PL/SQL, 커서와 예외처리 (0) | 2023.02.09 |
| 0208 오라클 DB 문제풀이 - 제약 조건 및 사용자, 권한, 롤 관리 (0) | 2023.02.08 |


