CP18 선형회귀
1) 선형회귀
단순회귀분석 (simple regression) : 독립변수가 하나, 종속변수는 하나
다중회귀분석 (multiple regression) : 독립변수가 2개 이상, 종속변수는 하나
- 회귀분석 : 오차를 가장 적게 만들어주는 선을 찾는 것을 의미함. (오차가 줄어야 예측하기가 쉬우니)
- 독립변수 = X변수
- 종속변수 = Y변수
최적선 : 주어진 데이터 셋의 데이터에 가장 잘 맞는 라인
회귀선 : 데이터 세트에서 두 변수 간의 관계를 추정하는데 사용되는 직선 (독립 변수 값을 기반으로 종속 변수 값을 예측)
예측 오차 : 종속 변수의 예측 값과 데이터 세트에서 실제 관찰된 값 간의 차이
2) 절편과 기울기
기울기 : X편차*Y편차합 / X편차제곱합 (X분산이 들어가는 이유는 Y가 얼마나 변하는지 보기 위함)
절편 : Y = bX + a -> a = y - bx
- y는 예측하려는 종속 변수(또는 응답 변수)입니다. (y평균)
- x는 y를 예측하는 데 사용하는 독립 변수(또는 예측 변수)입니다. (x평균)
- a은 절편(x가 0일 때 y의 값)이고,
- b은 기울기(x의 모든 단위 변화에 대한 y의 변화)입니다.
3) 회귀계수의 t검정
검정통계량 t 값 : 기울기 / 표준오차
대립가설 : 기울기 != 0
귀무가설 : 기울기 = 0
기울기가 높을 수록 예측치가 높음.
계산식 : sqrt ((yhat 편차제곱합 / 자유도) / x편차제곱합)
자유도 : n-k-1
n : 표본 크기
k : 독립 변수의 수(예측 변수)
4) 실습
# 단순선형회귀 simple regression
# 독립변수(x변수) 1개, 종속변수(y변수) 1개
x <- c(3.5,2.5,4.0,3.8,2.8,1.9,3.2,3.7,2.7,3.3)
y <- c(3.3,2.2,3.5,2.7,3.5,2.0,3.1,3.4,1.9,3.7)
# 평균
x_bar <- mean(x)
y_bar <- mean(y)
x_bar;y_bar
# 편차
# x편차 = x값 - x평균
x_dev <- x - x_bar
# y편차 = y값 - y평균
y_dev <- y - y_bar
# 기울기 = x편차*y편차 합/x편차 제곱합
b <- sum(x_dev*y_dev)/sum(x_dev^2)
b
# 절편 = y평균 - (기울기 * x평균)
a <- y_bar - b*x_bar
a
# 예측치 y hat
x = 2
y_hat <- b*x+a
y_hat
# 회귀계수(=기울기)에 대한 t검정
# 검정통계량 t값 = 기울기/표준오차
# 분자 = 기울기
b
# 분모 = 표준오차 = 제곱근((y hat 편차제곱합/자유도)/x편차제곱합)
# y hat 편차
# y hat = y 예측치 계산
y_hat <- b*x+a
y_hat
y_hat_dev <- y-y_hat
y_hat_dev
# y hat 편차제곱합
sum(y_hat_dev^2)
자유도 = n-k-1 (k:독립변수의 계수)
k <- 1
n <- length(x)
df <- n-k-1
k;n;df
# 분자 = (y hat 편차제곱합/자유도)
(sum(y_hat_dev^2)/df)
# 분모 = x편차제곱합
sum(x_dev^2)
# 제곱근(분자/분모)
se <- sqrt((sum(y_hat_dev^2)/df)/sum(x_dev^2))
se
# 검정통계량 t값 = 기울기 /표준오차
t <- b/se
t <- abs(t)
t
# 임계값, 유의수준, 자유도, 양측검정
alpha <- 0.05
df
cv <- qt(1-alpha/2,df)
cv
cv<t
True = 오른쪽 = 기각 = 귀무가설 기각 = 연구가설 채택
# 유의확률
1 - pt(t, df)
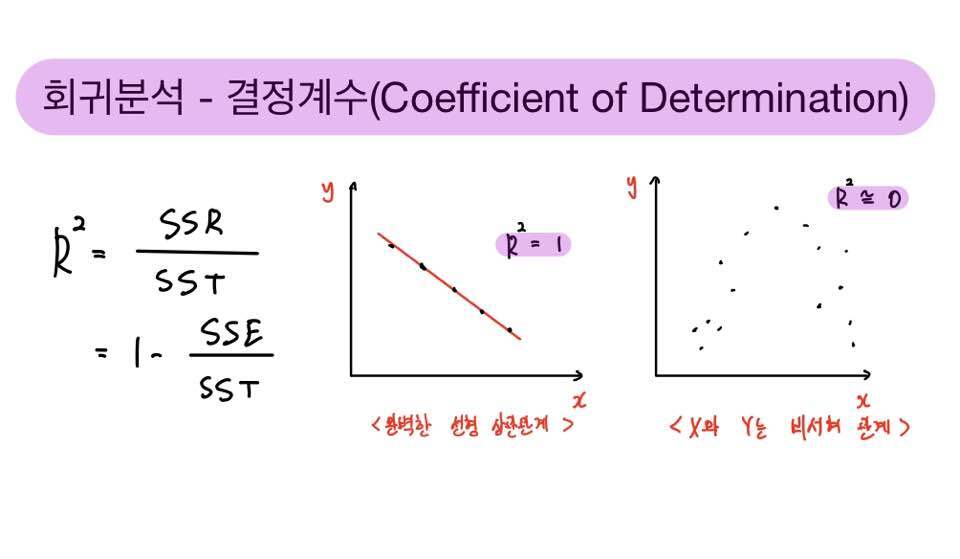
alpha > p5) 모형적합성 평가 : 결정계수 (모형 적합도)
* 결정계수 (총 변량)
- 설명력을 의미함
- 모형 설명된 변량 + 그렇지 못한 남은 변량
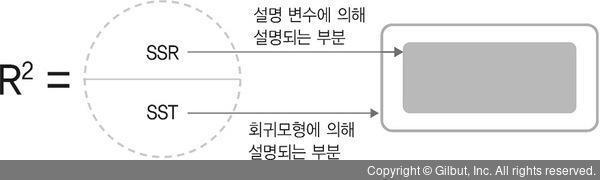
6) 결정계수의 계산
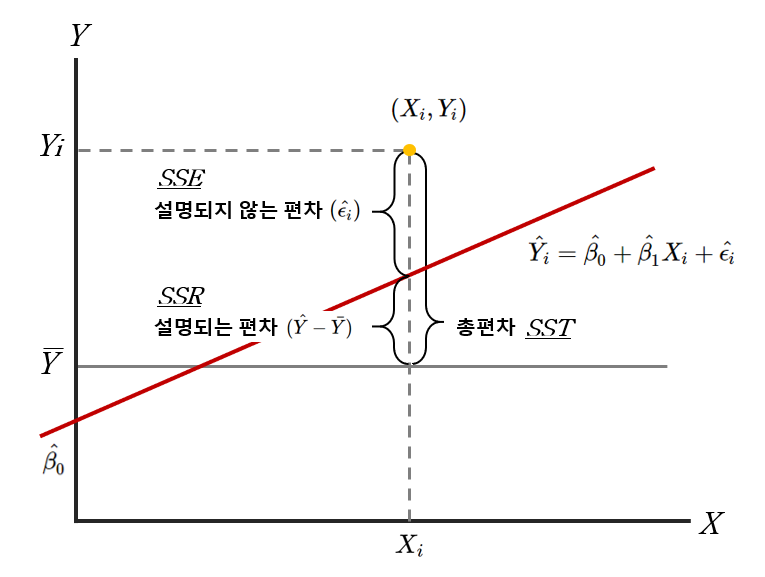
분산분석에서 BETWEEN -> 결정계수 ERROR
분산분석에서 WITHIN -> 결정계수 REGRESSION
SSR/SST = 1- SSE/SST
결정계수 값이 클 수록 좋은 것.
7) 결정계수 계산 실습
# 결정계수 = SSR/SST
# SSE
sse <- sum(y_hat_dev^2)
# SSR
# 회귀편차 = y hat - y평균
(y_hat-y_bar)
# 회귀편차제곱합 SSR
ssr <- sum((y_hat-y_bar)^2)
# 결정계수 = ssr/sst
ssr/(sse+ssr)
# 46% 설명할 수 있다.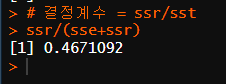
8) 조정 결정계수
- 수치가 높을 수록 모델의 적합성을 나타냄 (여러 모델의 적합도를 비교하는데 사용)
9) F검정의 절차
- 결론 : 해당 모델이 적합하다
10) 유의성 검정
p -> 1-pf(f,k,df)
alpha>p
11) 모형적합성 F검정 & 유의성 검정 실습
# 모형 적합성 F검정
# 검정통계량 F 값 = MSR/MSE
# MSR = SSR/K
msr <- ssr/k
# MSE = SSE/(n-k-1)
mse <- sse/df
f <- msr/mse
f
# 임계값, 유의수준, 자유도
k;alpha;df
cv <- qf(1-alpha,k,df)
cv
cv<f
# 연구가설 채택 = 회귀계수가 적어도 하나는 0이 아니다 = 유의하다
# 유의확률
p <- 1-pf(f,k,df)
p
alpha>p
sr <- lm(y~x)
summary(sr)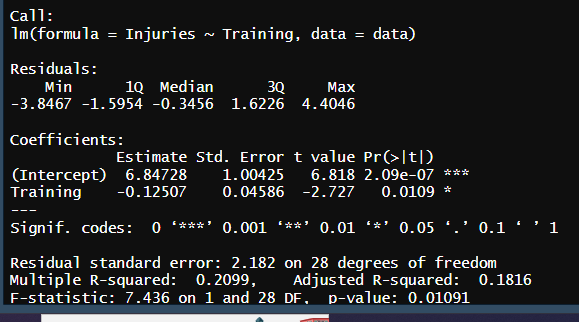
12) 예측 변수가 많으면 더 정확할까?
중요한 예측 변수가 많을 수록 정확도가 증가하지만 반대로
중요하지 않은 예측 변수면 정확도가 감소한다.
13) 다중회귀분석의 기본 개념
다중회귀분석 : 종속 변수 <-> 여러 독립 변수의 관계성
14) 다중회귀분석 실습
# 실습
data <- read.csv("./Syntax(R)/18/ch18ds1.csv")
head(data)
str(data)
단순선형회귀모델, lm(종속변수~독립변수)
sr <- lm(Injuries~Training, data = data)
summary(sr)
# 산점도+회귀선
plot(Injuries~Training, data = data)
abline(sr)
# 다중선형회귀모델
mr <- lm(Injuries~Training + Trainer, data = data)
summary(mr)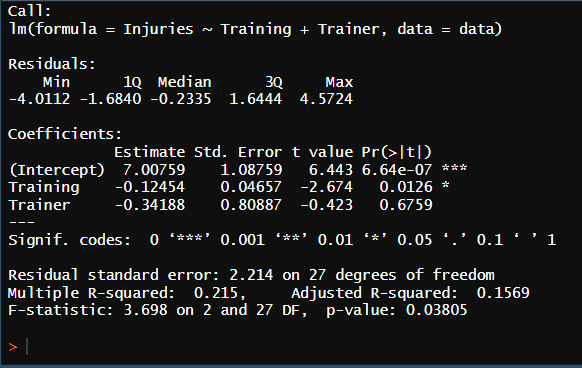
CP18 보건의료문제
1) 단순회귀모델

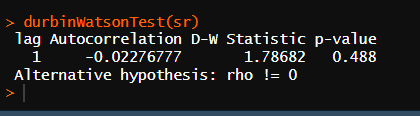
* 잔차의 독립성 검성 (d-w)
* 회귀분석 결과 표 확인
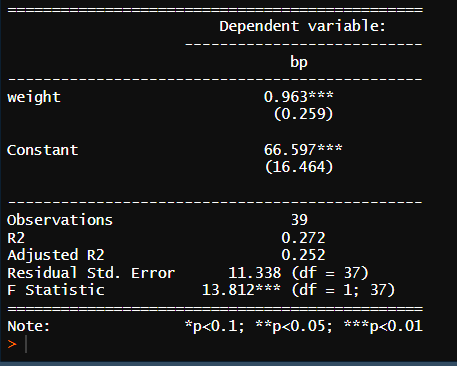
잔차의 독립성 검정 : 회귀모형의 오차나 잔차가 서로 독립적인지 여부를 확인하는 것
잔차 : 변수의 예측 값과 실제 값 간의 차이
잔차의 독립성 검정 쓰는 이유 : 잔차가 독립적이지 않다면 포착하지 못한 데이터의 구조나 패턴이 있음을 의미하기 때문에 잔차독립성을 검정한다
2) 다중 회귀 모델
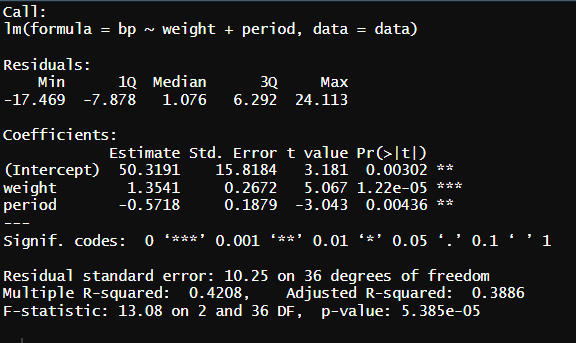
* 잔차의 독립성 검성 (d-w)

* 회귀분석 결과 표 확인

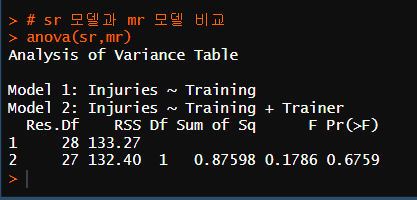
3) 다중 회귀 분석 결과표 작성
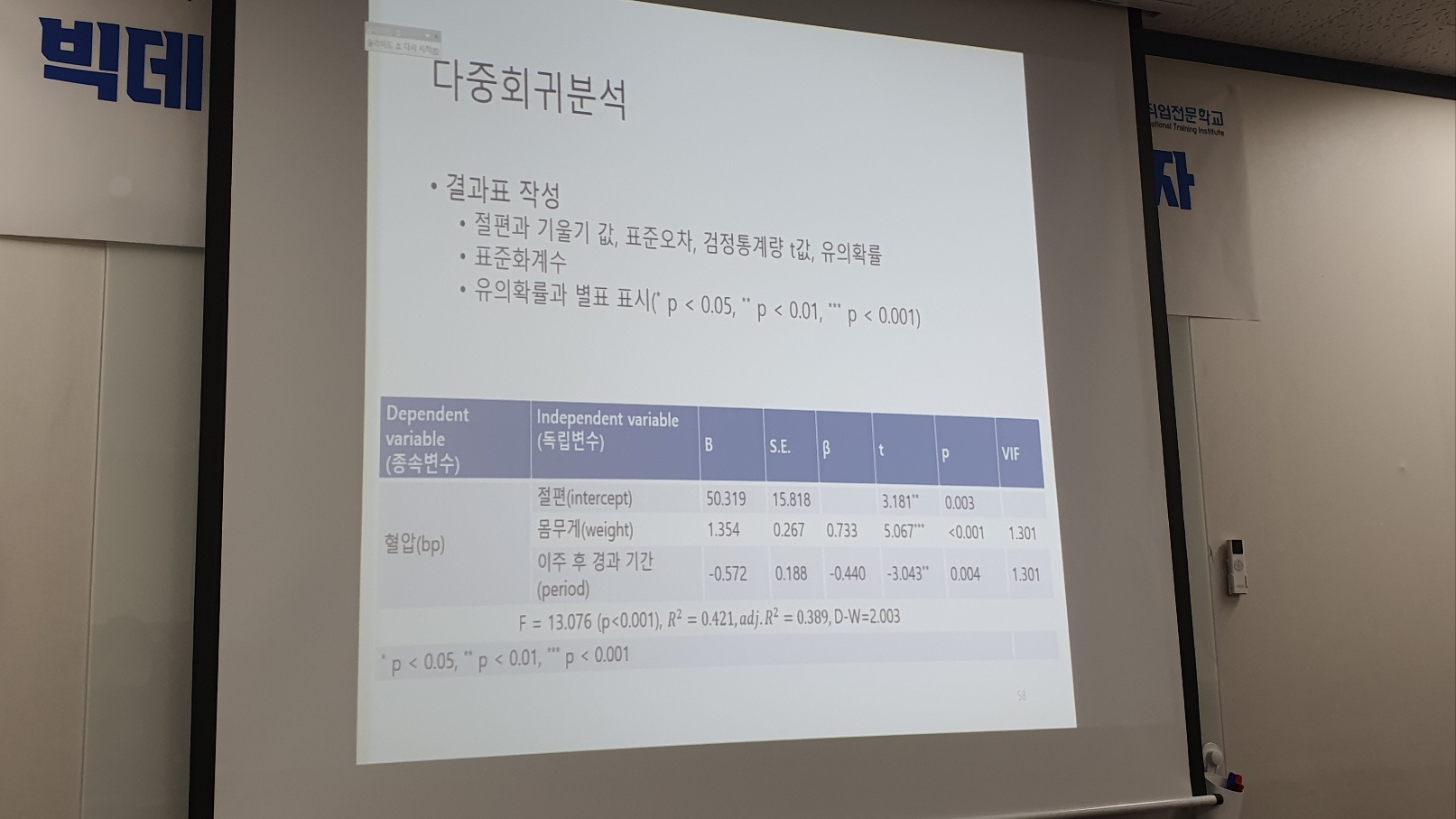
B / S.E. / b(베타) / t / p / vif
* 변수 정리
# 분모 = 표준오차 = 제곱근((y hat 편차제곱합/자유도)/x편차제곱합)
msr = (y hat 편차제곱합/자유도)
* 함수 정리
qf : 임계값 함수 (자유도 2개 필요) // 임계값 = 추계값
예시) qf(1-alpha,k,df)
pf : 누적 분포 함수 계산 (1-pf를 해서 f통계값을 구하기 위해)
예시) pf(f,k,df)
f는 f 통계 값
k는 모델의 예측 변수 수
df는 모델의 자유도
R-squared : 결정계수
adjusted : 조정
estimate 절편
training*estimate 회귀계수
검정 통계량 -> 임계값
'배운 책들 정리 > 만만한 통계 : R 활용' 카테고리의 다른 글
| 0223 만만한 통계 R 외부 챕터 15 - 내장 함수, 변수 타입과 데이터 구조 // 기초 문제 연습 (0) | 2023.02.23 |
|---|---|
| 0222 만만한 통계 R - 카이제곱 검정과 기타 비모수 검정 (CP19) (0) | 2023.02.22 |
| 0220 만만한 통계 R - 상관계수 계산 및 유의성 검정, 보건의료(7,17) (0) | 2023.02.20 |
| 0217 만만한 통계 R - 평균 차이 검정, 분산분석(ANOVA)(14,15) (1) | 2023.02.17 |
| 0216 만만한 통계 R - 독립 표본 t 검정, 종속 표본 t 검정 (0) | 2023.02.16 |



