0 목차 정리
- 확률과 유의성 검정이 중요한 부분
1 통계 입문
C1.통계에 대해
1) 통계를 통해 얻을 수 있는 것.
- 더 높은 학문을 위해 필요한 것, 보건 의료나 데이터 통계나 통용적으로 널리 쓰이는 것.
2) R을 쓰는 이유
- 시각화 기능 및 무료이기에
3) 통계의 역사
- 숫자의 발견 이후 의견의 결론을 주장하기 위한 자료로 쓰이게 됨.
* T 검정(20세기) : 두 집단의 평균 비교
* 상관계수(19세기) : 프렌치스 골턴이 상관계수를 정의했지만 피어슨이 음의 상관계수와 양의 상관계수를 정리하였다.
4) 통계의 범위
* 기술 통계 (평균, 중앙, 최빈값) : 전체 데이터에서 원하는 데이터로 결과값을 뽑기 위함. SQL에서 배운 것 그대로임.
연속형 변수(숫자) : 평균이나 중앙값으로 귀결할 수 있다.
범주형 변수(문자) : 빈도나 비율로 표현할 수 있고 최빈값으로 귀결할 수 있다.
* 추론 통계 : 모집단을 이해하기 위해서 하는 통계
모수 : 모집단의 특성 (모집단의 평균)
표본통계량 : 표본을 가지고 통계낸 것
변수 : 변하는 값을 의미함.
4-1) 변수 정리
* 연속형 변수 (양적 변수/숫자) : 등간 척도, 비율 척도
* 범주형 변수 (질적 변수/문자) : 명목 척도, 순위 척도
* 독립변수(원인) -> 종속변수 (결과)
예시) 종속변수가 혈압임 //
C2 R을 사랑하는 이유 및 프로그램 설치
설치를 했기 때문에 이 부분은 스킵.
2 R Studio 사용하기
C3. R Studio 사용하기
# 주석 = shift + ctrl + c
# 할당 연산자 = alt + -
# 명령어 실행 = ctrl + enter
a = 4
a <- 1
b <- 2
c <- 3
d <- 4
# 사칙연산
a+b
c-d
b*d
d/b
2*(a*b)
# 연산자를 넣으지 않으면 인식하지 못한다.
# combine 함수 : 여러 개의 값을 저장 (범용성 넓은 함수)
v <- c(1,5,7,9,2)
v1 <- c(1,2,3,4,5)
v2 <- c(1:5)
v2 <- c(1:5, 2)
v2
v6 <- c(2,4,6)
v6
# sequence 함수 : 연속적인 값만 만들 수 있다. 또는 특정 규칙에 따라 연속적인 값을 저장
v3 <- seq(1,5)
v3
v4 <- seq(1,10,by=2)
v4
# by는 간격을 의미 함. (by는 매개변수라 생략이 가능)
v4
# 문자
str1 <- "k"
str2 <- "text"
str3 <- c("a","b","c")
str4 <- c("hello!","world","is","good!")
str4
paste(str4,collapse ="_")
paste(str4,collapse =" ")
# 숫자 데이터 = 연속형 변수 = 평균
mean(v1)
# 문자 데이터 = 범주형 변수 = 비율
table(str3)
# 대괄호 : []
# 중괄호 : {}
# 소괄호 : ()
# 인덱스 : 데이터 위치
# 인덱싱 : 인덱스를 이용해 데이터 추출 작업
# 알파벳 추출 (index를 이용해서 뽑았기 때문에 indexing이라고 한다.)
LETTERS[1:20]
letters[c(11,15)]
LETTERS[c(16,1,18,11)]
LETTERS[c(10,9,9,14)]
L1 <- LETTERS[c(16,1,18,11)]
L2 <- LETTERS[c(10,9,9,14)]
L3 <- paste(L1,collapse = "")
L4 <- paste(L2,collapse = "")
# 파이썬에서는 가능하지만 R studio에서는 L3+L4을 적용해주는 기능이 없기에 paste로 적용한다.
paste(L3,L4, collapse = " ")
L3+L4
vv1 <- paste(v1, collapse = "")
vv1 <- paste0(v1, collapse = "")
vv1
v+v6
a1 <- 2*(3+5)
a2 <- (17+21)
a1
a2
# 제곱 = ^
2^2
2^4
(3+5)**2/17+21
(3+5)**2/(17+21)
# 하나의 열이라는 것을 이해해야함
correct <- c(8,6,5,8,7,8,9,6,10,8)
ls()
ls(pattern = "c")
ls(pattern = c)
# "" 표시를 안하면 알파벳을 숫자열로 인식해서 표시한다.
# 객체 지우기
# 1) 메뉴에서 Session - clear Workspace...
# 2) 아님 옆에 있는 빗자루 클릭
data1 <- c(45,56,34,56,25,74,35,68,98,56)
data2 <- c(7,5,3,6,4,7,6,4,5,9)
data3 <- c(1,2,1,2,2,1,2,1,2,2)
# 객체 확인
ls()
# 특정 객체 삭제
rm(data3)
# 외부 데이터 가져오기
# 창으로 선택해서 가져오기
read.csv(file.choose())
# 경로 설정으로 가져오기
# 작업 폴더 = 프로젝트 폴더 = ./
example <- read.csv("./Syntax(R)/03/Sample Data Set.csv")
example
str(example)
#
path = "./Syntax(R)/03/"
list.files(path, full.names = TRUE)
filenames <- list.files(path, full.names = TRUE)
filenames[3]
read.csv(filenames[1])
example <- read.csv("./Syntax(R)/03/Sample Data Set.csv")
example
# 간단한 기술 통계량 계산하기
# 연속형 변수에 해당하는 값들
# 최소값 = 0
# 1분위수 = 25분위수
# 2분위수 = 50분위수 = 중앙값(median)
# 3분위수 = 75분위수
# 최대값 = 4분위수 = 100분위수
# 평균
summary(example)
# 범주형 변수
example
# 빈도, 비율
table(example$Gender)
table(example$Treatment)
# 상관계수
data1
data2
cor(data1,data2)
# 산점도
plot(data1,data2)
# 패키지 검색
# 우하단의 Packages 창에서 검색
search()사용 했기 때문에 이 부분은 스킵. 감각을 잡는 느낌으로
과거에 했던거 다시 실행하면서 복습하는 시간.
3. 시그마 프로이트와 기술통계
C4. 평균 이해하기
1) 중심경향 측정값
- 중심경향 측정값 : 평균(mena), 중앙(median), 최빈값(mode)로 나눠짐
- 산포 척도 :
- 왜곡 척도 (왜도,첨도)
* 왜도 : 한쪽으로 쏠려있는지
* 첨도
2) 평균 계산하기 (정규분포를 가정하고 계산하는 모수통계를 구하기 위함)
시그마 ∑ : x의 값을 다 더하라는 뜻 (sum)
n : 평균에서 n은 시그마의 개수
3) 문제 (#유치원부터 초등학교 6학년까지 평균 학생수)
#Q1 95P
#유치원부터 초등학교 6학년까지 평균 학생수
# 변수 설정
x <- c(18,21,24,23,22,24,25)
x
# 계산식 (3가지 방법)
mean(x)
(18+21+24+23+22+24+25)/7
sum(x)/7
sum(x)/length(x)
round(mean(x),2)
4) 평균 키워드의 정의
μ (모평균) (모수의 평균) : 중앙값은 데이터 분포에 대한 정보를 제공하는 중심 경향의 척도입니다.
xbar (통계량) (표본평균) : 표본 평균은 모집단 평균의 추정치이며 표본에서 모집단을 추론하는 데 사용됩니다.
- 소문자 n : 평균이 계산 되는 표본 크기
- 대문자 N : 모집단 크기
- 평균은 이상치에 예민하다. 그래서 제거하는 경우가 많다.(이상치는 극단적인 값을 의미함)
- 편차 : 편차는 데이터 세트의 확산 또는 변동성을 측정하고 이상값을 식별하는 데 사용된다.- 산술 평균 : 편차의 합이 0이 되는 점- 평균 편차의 합은 0이어야 함.
5) 가중 평균 문제
# 가중평균 98P
score <- c(97,94,92,91,90,89,78,60)
freq <- c(4,11,12,21,30,12,9,1)
score*freq
sum(score*freq)/sum(freq)
#점수에 대한 산술평균
mean(score)
6) 중앙값 계산하기
# 중앙값 계산 99P
# 데이터 개수가 홀수일 때
hi1 <- c(135456,25500,32456,54365,37668)
sort(hi1)
# 데이터 개수가 짝수일 때
hi2 <- c(135456,54365,37668,34500,32456,25500)
sort(hi2)
median(hi2)
# 함수 적용
median(hi1);median(hi2)
(34500+37668)/2
# 중앙값 문제 100p (홀수)
s1 <- c(43,34,32,12,51,6,27)
sort(s1)
median(s1)

7) 극단치가 있는 경우
# 극단치가 있는 경우
x <- c(135456,54365,37668,32456,25500)
# 평균
mean(x)
# 중앙값
median(x)
# 극단치를 제외한 평균
mean(x[2:5])
# 히스토그램
hist(x)



- 1차원 그래프
막대그래프 : 범주형 변수
히스토그램 : 연속형 변수
* 히스토그램은 연속적인 값을 구간을 범주형처럼 나눴을 뿐 실제로는 연속형과 같이 붙어있음.
* 막대가 붙어 있으면 히스토그램
* 막대가 떨어져 있으면 산점도(막대그래프)
8) 최빈값 계산하기
- 가장 높은 값
- 바이라는건 이중값을 의미함
- 범주형 변수를 표현하는 값
- 정성적, 범주적, 명목적 데이터에 대한 중심경향 측정을 구할 수 있다.
9) 중심경향 값을 사용하는 경우 - 측정 척도
* 범주형 변수 // 최빈값
측정 척도에 따라 다름
명목척도 : 범주로 구분 되어 있는 값 (인종, 성별 등등) // 상호배타적 (독립 = 교집합 x)
서열척도(리커트 척도) : 순서, 순위를 나누는 척도
*연속형 변수
등간척도 : 간격이 모두 동일하는 것을 의미
비율 척도 : 절대 0이 있는 것을 의미 (아무런 특성도 없는 상태를 의미)
* 정확도
비율 > 등간 > 순위(서열) > 명목
이상치가 있다면 중앙값을 더 많이 쓰지만
일반적으로 정확도의 중요도는
평균 > 중앙값 > 최빈값으로 사용한다.
* 요약
- 낮은 정밀도의 척도를 정리후 순서대로 정밀한 척도 순으로 정렬
10) 배운거 정리하기
# 실습
data <- read.csv("./Syntax(R)/04/ch4ds1.csv")
head(data)
str(data)
# 기술통계량
# 평균
mean(data$Predjudice)
sum(data$Predjudice)/length(data$Predjudice)
# 중앙값
median(data$Predjudice)
# 최빈값
mode(data$Predjudice)
# 에러 수정
as.factor(data$Predjudice)
summary(as.factor(data$Predjudice))
table(as.factor(data$Predjudice))
# 요약통계량
summary(data$Predjudice)


C5. 변동성 이해하기
1) 변동성
# 변동성
# 편차
a <- c(7,6,3,3,1)
b <- c(3,4,4,5,4)
c <- c(4,4,4,4,4)
a_mean <- mean(a);b_mean <- mean(b);c_mean <- mean(c)
a_mean;b_mean;c_mean
# 편차 = 데이터 값(관측치) - 평균
a_dev <- a - a_mean;b_dev <- b - b_mean;c_dev <- c - c_mean
a_dev;b_dev;c_dev
# 편차의 합 = 0
sum(a_dev);sum(b_dev);sum(c_dev)
# 편차 제곱
a_dev2 <- a_dev^2;b_dev2 <- b_dev^2;c_dev2 <- c_dev^2
a_dev2;b_dev2;c_dev2
# 분산 = 편차제곱합 / (n-1)
bun <- sum(x_dev2) / (length(x)-1)
bun
# 표준편차 = 제곱근(분산) = sqrt(분산)
sqrt(sum(x_dev2) / (length(x)-1))
# 평균 ± 표준편차 = 6 ± 1.763834



편차가 같을 때 변동성을 측정하는 이유는 안정성과 예측 가능성을 얻기 위함이다.
연속형 분포를 보기 위해서는 변동성을 구하는 것이다.
2) 산포 척도 (얼마나 퍼져 있는지)
- 범위 : 최댓값 - 최소값
- 분산S^2 : 분산 = 표준편차^2
- 표준 편차 S : 분산을 제곱근 씌운 것.
3) 범위
- 재원일수 : 포용적 범위 h-l+1 (퇴원일-입원일+1) (양입법) // 배타적 범위 h-l (단입법)
4) 표준편차
- 평균+- 표준편차 = mean +- SD
- 통계 표본이 적을 경우 분모에서 n-1을 해야한다. 이래야 결과 값이 많아지기 때문이다.
- 어떤 표준으로부터 벗어난 정도를 의미
- sum(편차제곱) / n-1
- 표준편차가 크다는 것은 데이터가 많이 퍼져있다는 뜻.

X1 : 개별 점수
X_bar : 평균
N : 표본 크기
윗덩이 제곱까지는 분산 그걸 루트 씌우면 분산
- 표준편차는 연속형 분포를 구하기 위함.
5) n-1의 이유
- 표본값이 작아서 생기는 편차를 줄이기 위해서
6) 표준편차의 중요성
- 분산보다 표준편차로 표현하는게 더 쉽기 때문에
- 평균작업량의 차이를 구해서 표현하는게 표준편차가 더 쉬움,
- 표준편차 : 원래 단위로 떨어진 느낌
- 분산 : 제곱 단위로 떨어진 느낌
- 기술통계에서도 분산분석을 많이 쓰지 않지만 ANOVA나 회귀분석에서 많이 쓰이기 때문에
기술통계에서는 해석의 용이성을 위해 표준편차를 선호할 뿐 분산이 중요하지 않은 것은 아니다.
7) 문제 풀이 130p // 표준편차 구하기
# 문1 130p
data <- read.csv("./Syntax(R)/05/ch5ds1.csv")
head(data)
str(data)
x <-data$Reaction.Time
# 요약통계
summary(x)
# 범위 = 최대값 - 최소값
max(x)-min(x)
# 분산 = 편차제곱합 / (n-1)
# 편차 = 값 - 평균
mean <- mean(x)
mean
dev <- x-mean
dev
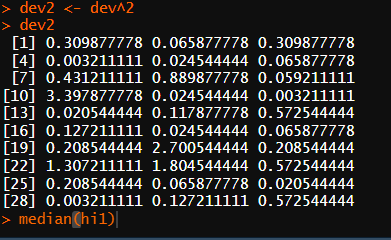
# 편차제곱
dev2 <- dev^2
dev2
# 분산 = 편차제곱합 / (n-1)
# 편차 제곱합
sum(dev2)
# 표본 크기
length(x)
# 분산
sum(dev2)/(length(x)-1)
# 표준편차 = 제곱근 (분산) = sqrt(분산)
sqrt(sum(dev2)/(length(x)-1))
#함수
var(x)
sd(x)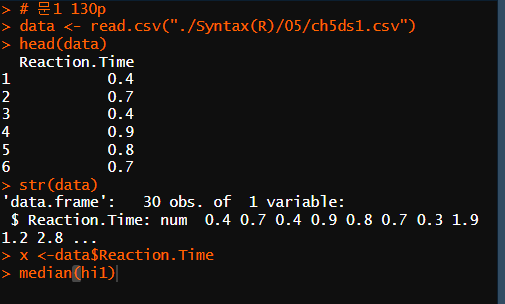




7) 문제 풀이 135p // 기술통계량
# 실습// 기술통계량
data <- read.csv("./Syntax(R)/05/ch5ds2.csv")
head(data)
str(data)
x <- data$Math.Score
x1 <- data$Reading.Score
# 범위
range(x)
range(x1)
# 요약통계량
# install.packages("psych")
library(psych)
describe(x)
describe(x1)

핵심
- 기술통계 (중심경향 값) : 평균, 중앙, 최빈값
- 추론통계 : 모집단과 표본
- 범주형 : 중앙값(극단적인 이상치에서는 평균이 왜곡 되기 때문에 중요), 최빈값
- 연속형 : 평균 (가장 정확함)
- 산포척도 (얼마나 퍼져있는지) (변동성)
범위 : 최댓값 - 최소값
분산 (var) : 분산 = 표준편차^2
표준 편차 (sd) : 분산을 제곱근 씌운 것.
* 표준 편차 구하는 순서
데이터 입력 (data,head,str) -> 요약 통계 (summary) -> 범위 (max-min) ->
분산을 위한 식 (x-mean(x))^2/(length(x)-1) -> 표준편차 (sqrt)
* 함수 정리
mean : 평균
mode : 최빈값
median : 중앙값
var : 분산
sd : 표준편차
'배운 책들 정리 > 만만한 통계 : R 활용' 카테고리의 다른 글
| 0220 만만한 통계 R - 상관계수 계산 및 유의성 검정, 보건의료(7,17) (0) | 2023.02.20 |
|---|---|
| 0217 만만한 통계 R - 평균 차이 검정, 분산분석(ANOVA)(14,15) (1) | 2023.02.17 |
| 0216 만만한 통계 R - 독립 표본 t 검정, 종속 표본 t 검정 (0) | 2023.02.16 |
| 0215 만만한 통계 R - 유의성 검사 및 단일 표본 z 검정 (11,12) (0) | 2023.02.16 |
| 0214 만만한 통계 R - 가설검정, 확률의 중요성 (09,10) (0) | 2023.02.14 |


