C13. 독립 표본 t 검정
# 독립표본 t검정 (등분산가정) // 양측검정
data <- data.frame(group1 = c(7,5,5,3,4,7,3,6,1,2,10,9,3,10,2,8,5,5,8,1,2,5,1,12,8,4,15,5,3,4),
group2 = c(5,3,4,4,2,3,4,5,2,5,4,7,5,4,6,7,6,2,8,7,8,8,7,9,9,5,7,8,6,6))
head(data)
str(data)
# 평균
g1_m <- mean(data$group1)
g2_m <- mean(data$group2)
g1_m;g2_m
# 표본의 크기
n1 <- length(data$group1)
n2 <- length(data$group2)
n1;n2
# 분산
var1 <- var(data$group1)
var2 <- var(data$group2)
var1;var2
# 등분산가정
# 통합분산추정치 = df1*var1 + df2*var2 / (df1+df2)
# ((1집단(자유도*분산)) + 2집단(자유도*분산))/ 자유도1+자유도2)
# df = 자유도 // var = 분산
df1 <- n1 -1
df2 <- n2 -1
df1;df2
# 분자 = (df1*var1+df2*var2)
(df1*var1 + df2*var2)
# 분모 df1+df2
(df1+df2)
# 통합분산추정치 = 분자/분모 = sp2
sp2 <- (df1*var1 + df2*var2) / (df1+df2)
sp2
# 검정통계량 t값
# 분자 = (g1_m - g2_m)
(g1_m - g2_m)
# 분모 = 제곱근 (sp2/n1+sp2/n2)
sqrt(sp2/n1+sp2/n2)
# 분자/분모
t <- (g1_m - g2_m)/sqrt(sp2/n1+sp2/n2)
t <- abs(t)
t
# 임계값
# 유의수준 0.05, 양측검정, df1+df2 = n1 + n2 -2
alpha <- 0.05
df <- df1+df2
alpha;df
cv <- qt(1-alpha/2,df)
cv<t
# FALSE = 채택역 = 귀무가설 채택 = 연구가설 기각 = 차이가 없다
# = 통계적으로 유의한 차이가 없다.
# 유의확률
# 한쪽 꼬리에 대한 유의확률 ()*2를 해서 양측 검정
p <- (1 - pt(t,df) )*2
p
alpha > p
data <- read.csv("./Syntax(R)/13/ch13ds1.csv")
head(data)
str(data)
# 그룹의 빈도표
table(data$Group)
# 등분산 분석 = var.test(종속변수(결과-특성)~독립변수(원인-그룹))
var.test(data$MemoryTest~data$Group)
# 귀무가설 : 두 분산이 같다(=차이가 없다) => var.equal=T
# 연구가설 : 두 분산이 같지 않다 (=차이가 있다) => var.equal=F
# 이분산 가정 독립표본 t검정 = t.test(종석변수~독립변수)
t.test(data$MemoryTest~data$Group, var.equal=F)
# 상자수염그림
boxplot(MemoryTest~Group, data = data)
# 상자수염그림
bp <- boxplot(MemoryTest~Group, data = data,
main = "Memory score by groups",
xlab="Groups",
ylab = "Memory socres")
bp
# bp <- boxplot(MemoryTest~Group, data = data)
bp
# 수염의 아래 끝, 1분위, 2분위(=중앙값), 3분위, 수염의 위 끝
bp$stats
# 예) 1번 그룹의 중앙값
# 인덱스번호 [행번호,열번호]
bp$stats[3,1]
# 예) 2번 그룹의 수염 끝 아래, 위
bp$stats[1,2];bp$stats[5,2]
bp$stats[c(1,5),2]
data2 <- read.csv("./SpyderBD_01/data/sta_data.xlsx")
data2
# 실습
options(scipen = 99)
# 데이터 준비
install.packages("readxl")
library(readxl)
data <- read_excel("./SpyderBD_01/data/sta_data.xlsx"
, sheet = "ind_t")
head(data)
str(data)
table(data$group)
# 등분산분석
t <- var.test(data$pain~data$group)
# 등분산가정
t.test(data$pain~data$group,var.equal = T)
# 기술통계 확인 (pain에 대한)
# 표본의 크기, 평균, 표준편차
install.packages("psych")
library(psych)
describe(data$pain)
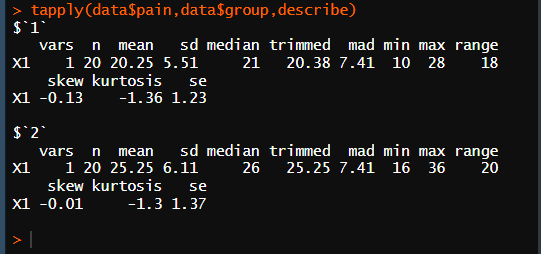
tapply(data$pain,data$group,describe)
# 기술통계표
install.packages("moonBook")
library(moonBook)
mytable(group~pain,data,digits=2)
# 짝지은 표본 t 검정
pre <- c(3,5,4,6,5,5,4,5,3,6,7,8,7,6,7,8,8,9,9,8,7,7,6,7,8)
post <- c(7,8,6,7,8,9,6,6,7,8,8,7,9,10,9,9,8,8,4,4,5,6,9,8,12)
# 차이값, 평균, 표준편차, 표번의 크기
diff <- post-pre
diff
diff_m <- mean(diff)
diff_m
diff_sd <- sd(diff)
diff_sd
n <- length(diff)
n
# 검정통계량 t값
# 분자 = diff의 평균 - 0
diff_m
# 분모 = 표준오차 = diff의 표준편차/제곱근(n)
diff_sd/sqrt(n)
# 분자/분모
t <- diff_m/(diff_sd/sqrt(n))
t
# 임계값
# 유의수준, 양측검정, 자유도
alpha <- 0.05
df <- n-1
cv <- qt(1-alpha/2,df)
cv
cv<t
# TRUE = 오른쪽 = 기각역 = 귀무가설 기각 = 연구가설 채택
# = 차이가 있다 = 통계적으로 유의한 차이가 있다.
#
# 유의확률
# alpha = 0.05
pv <- (1-pt(t,df))*2
alpha>pv
# TRUE = 오른쪽 = 기각역 = 귀무가설 기각 = 연구가설 채택
# = 차이가 있다 = 통계적으로 유의한 차이가 있다.
#
# 실습
data <- read.csv("./Syntax(R)/14/ch14ds1.csv")
head(data)
str(data)
diff <- data$Posttest-data$Pretest
diff
diff_m <- mean(diff)
diff_m
diff_sd <- sd(diff)
diff_sd
n <- length(diff)
n
# 짝지은 표본 t검정, t.test (paired=T)
t.test(data$Posttest,data$Pretest,paired = T)
# 산점도
plot(data$Pretest,data$Posttest,
main = "Scatter plot of pretest and psttest",
xlab = "Pretest score",
ylab = "Posttest socre")
# 상관계수
cor(data$Pretest,data$Posttest)1) 독립 표본 t 검정 테스트
독립 표본 t검정 테스트 : 두 독립 표본의 평균을 비교하려는 경우에 사용된다. 독립 표본 t-검정은 치료군과 대조군과 같은 두 개의 독립적인 환자 그룹의 평균을 비교하여 특정 조건에 대한 두 가지 다른 치료의 효과를 비교하는 데 사용할 수 있다. (t분포는 좌우대칭이다.)
* 귀무가설 = 모 평균
* 연구가설 = 표본 평균
2) T 검정 통계량의 8단계 계산 과정
- 귀무 가설 및 대립 가설 정의(등분산 분석): 귀무 가설은 일반적으로 두 독립 그룹의 평균 사이에 유의한 차이가 없다는 것을 나타내는 반면, 대립 가설은 유의한 차이가 있음을 나타냅니다.
- 유의 수준(알파) 및 자유도(df) 결정: 알파 수준은 일반적으로 0.05로 설정되며, 이는 제1종 오류를 범할 확률이 5%임을 의미합니다(귀무 가설이 참일 때 기각). . 자유도는 n1 + n2 - 2와 같습니다. 여기서 n1과 n2는 두 그룹의 샘플 크기입니다.
- 데이터를 수집하고 표본 평균(x̄1 및 x̄2)과 표본 표준 편차(s1 및 s2)를 계산합니다. 이러한 통계는 두 그룹의 중심 경향과 변동성을 설명합니다.
- 평균 차이의 표준 오차(SE) 계산: 표준 오차는 다음 공식을 사용하여 계산됩니다. SE = √((s1^2/n1) + (s2^2/n2)).
- 검정 통계량(t) 계산: 검정 통계량은 다음 공식을 사용하여 계산됩니다. t = (x̄1 - x̄2) / SE.
- t의 임계값 결정: 이것은 알파 수준과 자유도에 따라 다릅니다. 예를 들어, alpha = 0.05 및 df = 18인 경우 t의 임계값은 ±2.101입니다.
- 검정 통계량을 임계값과 비교: 검정 통계량의 절대값이 임계값보다 크면 귀무가설이 기각되고 대립가설이 채택됩니다.
- 결과 해석: 귀무 가설이 기각되면 두 그룹의 평균 사이에 유의미한 차이가 있음을 의미합니다. 차이의 크기는 Cohen의 d 또는 Hedges의 g와 같은 효과 크기를 사용하여 정량화할 수 있습니다.
* 등분산가정 문제 (310p, 318p)
알츠하이머 환자를 대상으로 그룹 1은 영상자료를 활용해 수강 그룹 2는 영상을 보며 동시에 입으로 되뇌라는
지시를 했을 때 기억력의 차이가 있는가?
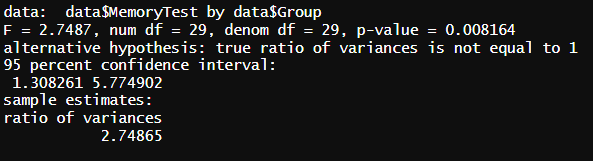
기억력의 차이가 있는지 두 그룹의 대립가설을 확인하고자 했다. (두 분산이 같지 않다는 것을 확인하고자)
p-value(유의성)가 0.05 이하로 유의성이 있기 때문에 대립가설이 채택이 되었다.
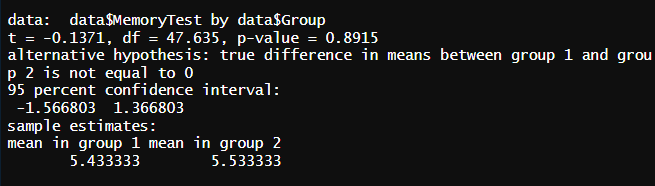
두 그룹 간의 유의성을 확인해봤더니 0.8이 나왔기 때문에 유의하지 않다는 것으로 귀결되어
귀무가설이 채택 되어 기각역이 되었다.
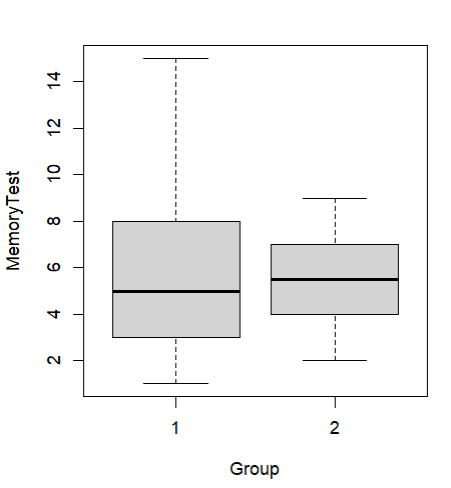
수염 위 아래 부분은 이상치에 해당 되고 막대 첫 부분부터 마지막까지 선이 3개이기 때문에 3쿼터로 나뉜다.
* 1번 더
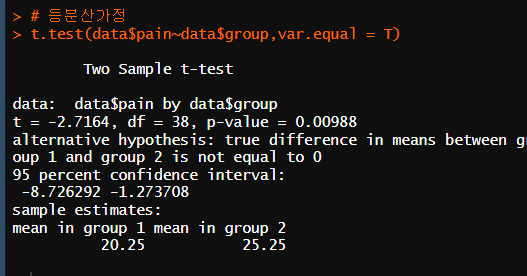
등분산가정을 했을 때 p-value가 0.05이하이므로 귀무가설 기각역에 해당 되기에
대립가설이다. (연구가설에서 증명하고자 한 가설이 의미가 있다.)
* pain에 대한 기술통계 (tapply 함수를 이용한) // 독립 표본 t 검정
C13 종속 표본 T 검정
* 종속 표본 t검정 검정 통계량 공식

검정통계량 해당 공식으로 외우기
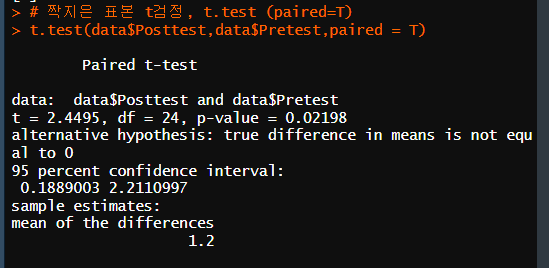
t.test를 활용해서 두 가지 점수 집합 간에 유의미한 차이가 존재한다고 결론 내릴 수 있는지를 확인하기 위함
* 핵심
- 독립 표본 t 검정
- 종속 표본 t 검정
'배운 책들 정리 > 만만한 통계 : R 활용' 카테고리의 다른 글
| 0220 만만한 통계 R - 상관계수 계산 및 유의성 검정, 보건의료(7,17) (0) | 2023.02.20 |
|---|---|
| 0217 만만한 통계 R - 평균 차이 검정, 분산분석(ANOVA)(14,15) (1) | 2023.02.17 |
| 0215 만만한 통계 R - 유의성 검사 및 단일 표본 z 검정 (11,12) (0) | 2023.02.16 |
| 0214 만만한 통계 R - 가설검정, 확률의 중요성 (09,10) (0) | 2023.02.14 |
| 0213 만만한 통계 R - 기술 통계(평균,중앙,최빈값), 표준편차, 분산 (0) | 2023.02.13 |


