1. 선형회귀와 로지스틱 회귀분석의 차이점과 문제점을 알려줘


선형회귀와 로지스틱 회귀분석의 차이점은 크게 세 가지가 있습니다.
종속 변수의 형태 선형회귀는 연속형 변수를 예측하는데 사용되며, 종속 변수는 연속형 값이어야 합니다.
반면 로지스틱 회귀분석은 이항 분류 문제에 사용되며, 종속 변수는 이항 변수(0 또는 1)로 표현됩니다.
예측 방법 선형회귀는 종속 변수와 독립 변수 간의 선형 관계를 모델링합니다.
독립 변수의 값이 증가할 때 종속 변수도 증가하거나 감소합니다.
반면 로지스틱 회귀분석은 로지스틱 함수를 사용하여 종속 변수의 확률 값을 예측합니다.
로지스틱 함수는 S 자 형태의 곡선으로, 독립 변수의 값에 따라 종속 변수의 값을 0과 1 사이로 제한합니다.
모델 해석 선형회귀는 각 독립 변수가 종속 변수에 얼마나 영향을 미치는지를 쉽게 이해할 수 있습니다.
반면 로지스틱 회귀분석은 독립 변수의 영향을 해석하기가 어렵습니다.
로지스틱 함수가 S자형태의 곡선이기 때문에, 각 독립 변수가 종속 변수에 미치는 영향은 독립 변수의 값이 다른 변수에 따라 달라질 수 있습니다. 문제점으로는 이상치(outliers)에 민감하다는 것입니다.
이상치가 존재하면 모델의 예측 성능이 크게 저하될 수 있습니다. 또한, 과적합(overfitting)이 발생할 수 있습니다. 과적합은 모델이 학습 데이터에 너무 맞춰져서 새로운 데이터에 대한 예측 능력이 떨어지는 문제입니다. 따라서, 적절한 모델 선택과 데이터 전처리가 중요합니다.
2. 연속형 변수와 이항 변수의 예시를 들어줄래

연속형 변수의 예시로는 키, 몸무게, 온도 등이 있습니다. 이들 변수는 값이 연속적으로 변하며, 측정 단위에 따라 소수점 이하의 값을 가질 수 있습니다. 이항 변수의 예시로는 성별, 흡연 여부, 결혼 여부 등이 있습니다. 이들 변수는 값이 두 가지 중 하나로 분류되며, 범주형 변수에 해당합니다. 0 또는 1과 같은 이진 값으로 표현될 수 있습니다.
3. 모형 평가에 대한 설명




모형 평가란 데이터 분석에서 모형의 성능을 평가하는 것을 말합니다.
이때, confusion matrix는 모형의 성능을 평가하는데 많이 사용되는 도구입니다.
Confusion matrix는 모형이 예측한 결과와 실제 결과를 비교하여 4가지 요소로 나누어 표현하는 행렬입니다.
이 4가지 요소는 다음과 같습니다.
True Positive(TP): 모형이 양성(positive)이라고 예측하고, 실제로도 양성인 경우
False Positive(FP): 모형이 양성이라고 예측했지만, 실제로는 음성(negative)인 경우
False Negative(FN): 모형이 음성이라고 예측했지만, 실제로는 양성인 경우
True Negative(TN): 모형이 음성이라고 예측하고, 실제로도 음성인 경우
이 4가지 요소를 이용하여 다양한 성능 지표를 계산할 수 있습니다. 예를 들어, 모형의 정확도(Accuracy)는 TP와 TN의 비율로 계산할 수 있습니다. 민감도(Sensitivity)는 TP의 비율로 계산하며, 특이도(Specificity)는 TN의 비율로 계산할 수 있습니다. 이처럼 confusion matrix는 모형의 성능을 평가하고 개선하는데 매우 유용한 도구입니다. 따라서 데이터 분석에서는 이를 적극적으로 활용하여 모형의 성능을 높이는 것이 중요합니다.
4. 머신러닝 - 결정 트리 구조 (시각화 이미지 참고하여)


머신러닝에서 결정 트리는 데이터를 분석하고 예측하기 위한 분류 모델 중 하나입니다.
결정 트리는 데이터의 속성들을 기반으로 하나의 속성을 선택하고,
그 속성에 대한 기준값을 정하여 데이터를 분할합니다.
이렇게 분할된 데이터는 다시 동일한 과정을 반복하여 나무 가지처럼 계속 분할해 나가면서
최종적으로 예측 결과를 도출합니다.
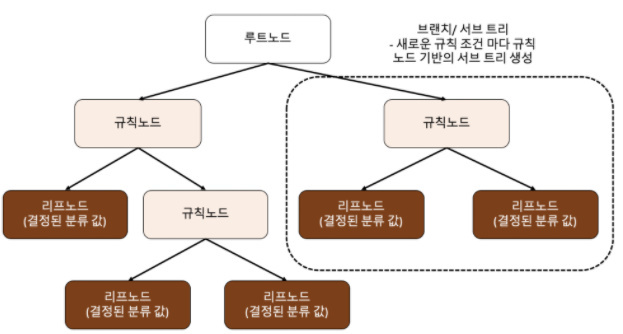
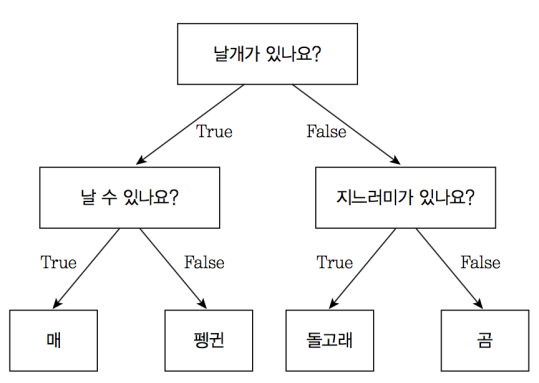
결정 트리의 구조는 시각화 이미지를 통해 쉽게 이해할 수 있습니다.
맨 위에는 뿌리 노드(root node)가 위치하고, 이어지는 가지(branch)들과 마지막에는 잎 노드(leaf node)들이 위치합니다. 각 노드는 데이터를 분할하기 위한 속성과 기준값을 가지고 있습니다.
속성은 노드의 위치에 따라 분할에 사용된 속성이 달라집니다.
예를 들어, 아이리스(꽃) 데이터를 분류하는 결정 트리의 구조를 시각화하면, 맨 위에는 꽃잎(petal)의 길이가 위치하고 그 다음 가지에서는 꽃잎의 너비와 길이 비율에 대한 기준값을 설정합니다. 이렇게 결정 트리를 따라 내려가면서 각 노드가 어떤 속성과 기준값을 가지는지에 따라 데이터가 분할되고, 결국 분류 결과를 도출합니다. 결정 트리는 데이터의 분류 과정이 시각적으로 보여지기 때문에 이해하기 쉽고, 모델의 결과를 해석하는 것이 쉽다는 장점이 있습니다.
또한, 다른 분류 모델들과 비교해 빠른 속도로 학습이 가능하다는 점도 장점입니다.
5. 머신러닝에서의 엔트로피 불순도와 지니 불순도에 대해



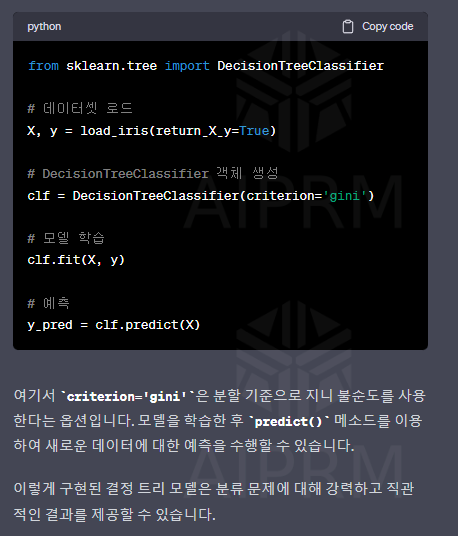
머신러닝에서 결정 트리 알고리즘을 사용할 때, 데이터를 분류하기 위해 불순도를 측정합니다.
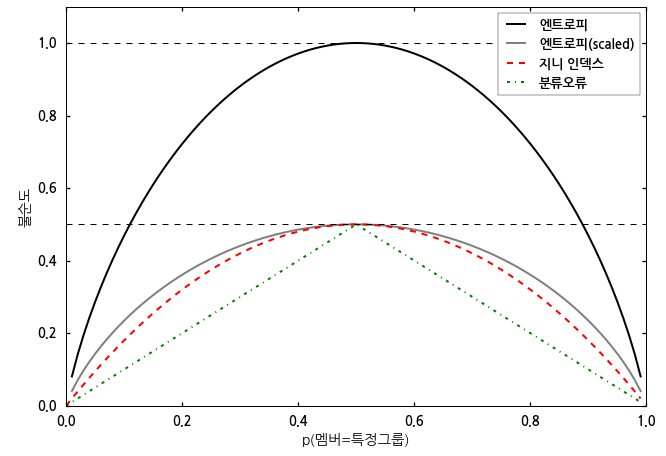
이때 사용되는 대표적인 불순도 지표로는 엔트로피 불순도와 지니 불순도가 있습니다.
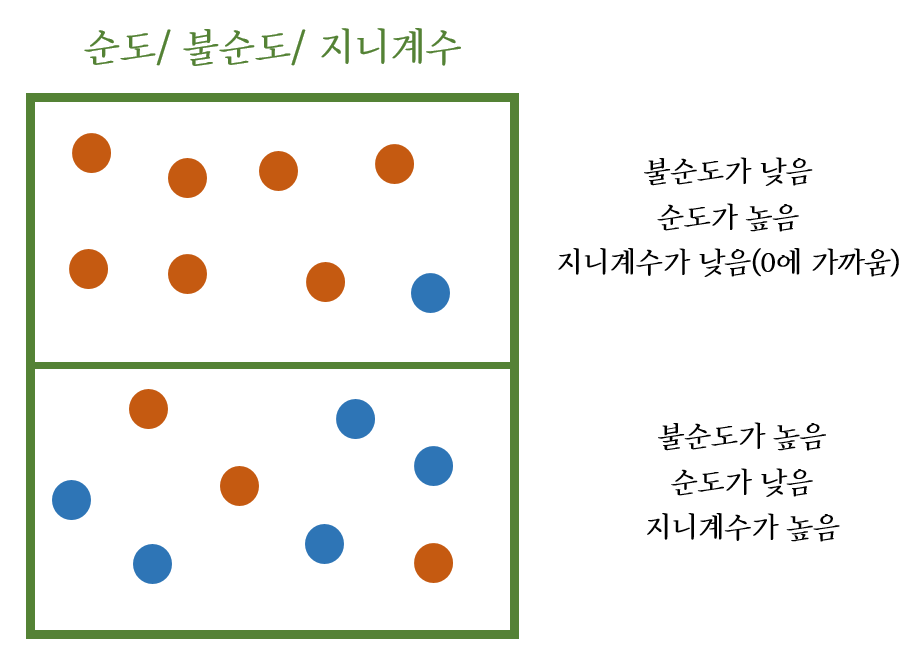
엔트로피 불순도는 정보 이론에서 유래한 개념으로, 어떤 집합의 혼잡도를 나타내는 지표입니다.
불순도가 높을수록 혼잡한 집합이므로, 엔트로피 불순도가 높을수록 데이터의 분류가 어려워집니다.
지니 불순도는 엔트로피 불순도와 비슷한 개념으로,
데이터가 다양한 값을 가질수록 불순도가 높아지는 것을 측정하는 지표입니다.
이는 엔트로피 불순도와 마찬가지로, 불순도가 높을수록 분류가 어려워지는 경향이 있습니다.
둘 다 불순도를 나타내는 지표이지만, 엔트로피 불순도는 정보 이론에서 유래하였고,
지니 불순도는 CART(Classification And Regression Tree) 알고리즘에서 사용됩니다.
결정 트리에서는 이 둘 중에 어떤 지표를 선택해서 사용할지, 혹은 둘을 섞어서 사용할지는 사용자가 결정합니다.
'개인공부 정리 > 다양한 질문들' 카테고리의 다른 글
| 자바의 정석 4,5 질문 - 조건문,반복문,배열 2 (0) | 2023.05.13 |
|---|---|
| 파이썬 머신러닝 판다스 데이터 분석 6,7 질문 - 데이터프레임의 다양한 응용, 머신러닝 데이터 분석 (0) | 2023.05.01 |
| 파이썬 머신러닝 판다스 데이터 분석 4_3, 5 질문 - 시각화, 데이터 사전 처리 - zip함수와 enumerate 함수의 차이점 (0) | 2023.04.27 |
| 혼자 공부하는 파이썬 4 질문 - 문자열, 리스트, 딕셔너리와 관련된 기본 함수(while,range,reversed,enumerate,Counter 등등) (0) | 2023.04.14 |
| 혼자 공부하는 파이썬 2,3,4 질문 - 숫자와 문자열의 다양한 기능, 조건문, 반복문 (0) | 2023.04.11 |


